トモです、こんにちは。
最近思ったのですが、3次元の変な形を作れるように最適化するという案件が去年の暮れから今年にかけていくつかあったので、自分なりにノウハウを纏めようと思いました。
私はあまり深くRHINOCEROS(ライノ)とかGrasshopper(GH)を触っているわけではないのですが、それでも何とかお仕事に携われることができています。
私がどのようにライノとGHを使っているか、何をしているのかとか、今まで書いてこなかったので書いてみようと思います。
目次
RhinoとGrasshopperで複雑な形をどうやって伝えるか
例えば上のような形を設計者ってライノとGHを駆使して作るわけですね。
これは複雑そうに見えて、実は作るの簡単じゃねーか、ってライノとGHに精通している方は思うかもしれませんが。。。
実際大したことはやってないのですけど、これどうやって作ったかっていうのはさておき、設計者としては、これをどうやって図面化して施工者に伝え、最終的にファブリケーションまで持っていくかということを考えないといけないです。
ここで重要なポイントが2つあります。
重要ポイント
- 1.どのようにこの形状を再現性がある状態で設計図書に記録し施工者へ伝えるか
- 2.施工者がこれを作る上でどうやったら安く作ることができるか
この2ポイントについて、私のわかる範囲でなるべく詳しく書きたいと思います。
設計図書にどのように記載するべきか
再現性があるか
まずはですね、自分で複雑な形を作ったらそれがどのような形状かを設計図書に載せておかないといけませんね。
ここでキーポイントになるのは再現性があるかどうかです。
要するに設計図書だけを見た時にその全く同じ形が再現できるだけの情報をきちんと載せられているかというところが問われるわけです。
こんなこと言うと怒られるかもしれませんが、私の経験上はこのプロセスは建築を作る上ではあんまり重要ではないと思ってます。
もちろんこの時点で形の整合性が取れているかを確認するのはとても重要な事なのですが、実際に設計図書の数字を追って施工者が施工することは少ないと感じているからです。
それは何故かというと、日本では施工者と設計者の間の距離が近く、暗黙の了解みたいなことがあり、施工者から「当然モデルあるんですよね?」という打診が入り、設計側は「設計図書の通りに作ってくださいね、モデルを使ったことによる諸々の責任は取りませんが参考までにモデル送ります」というやり取りが交わされたりすることがあるのです。
形状定義するメリット
ここで何らかのトラブルが起こった場合のことを想定すると、設計図書に再現性のある情報を載せているかということが、争点の一つになります。
よってトラブルになった場合は後々、施工者にいちゃもんを付けられるようにきちんと形状を載せておくことに意味はあります。
が、しょせん、モデルありきで作るので、結局設計図書に載っている数字はトラブルにならない限り参照されることはないのかななんて思ったりしてます。
後の施工者とのやり取りの方がよっぽど重要です。
施工者サイドから、VE案(ヴァリュー・エンジニア)といって安い代替案とかが出てくるので、そこでどれだけ設計者として形を守れるかという攻防戦が繰り広げられることになります。
設計図書には最低限の情報を載せておく
まずは、施工者とのファブリケーションの話の前にまずは、設計図書ですね。
これに何を記載しておけばよいのかということを考えたいと思います。
ここで考慮すべきなのは円弧近似と座標で形の原則を示してあげることだと思います。
細かなパネル割りとかそういうことは施工サイドの都合で決まってくることが多いので、最低限の幾何学的形状を伝えるというのが正しいのではないかと思います。
設計者側としてはなるべく少ない情報で形状を定義することで細かな責任を負わないということと、施工者にデザインの意図(要点)だけを伝えるのが目的です。
有機的な形の場合は円弧近似をする場合が多い
幾何学といっても方程式で全部のカーブを説明するのは現実的ではないので、どこかに中心をもつ円弧の部分でカーブを近似してあげて、その半径と中心点を定義することで、設計図書とすることがありました。
私は東南アジアの某タワーでそのような仕事に携わることがありまして、その時はそのように進めました。それが一般的かどうかは分かりません。
今やっている仕事でも円弧近似でなるべくパターンを少なくすることで施工コストが抑えられるみたいな話があるので、それなりに理にかなってはいると思います。
円弧近似はなぜ必要か
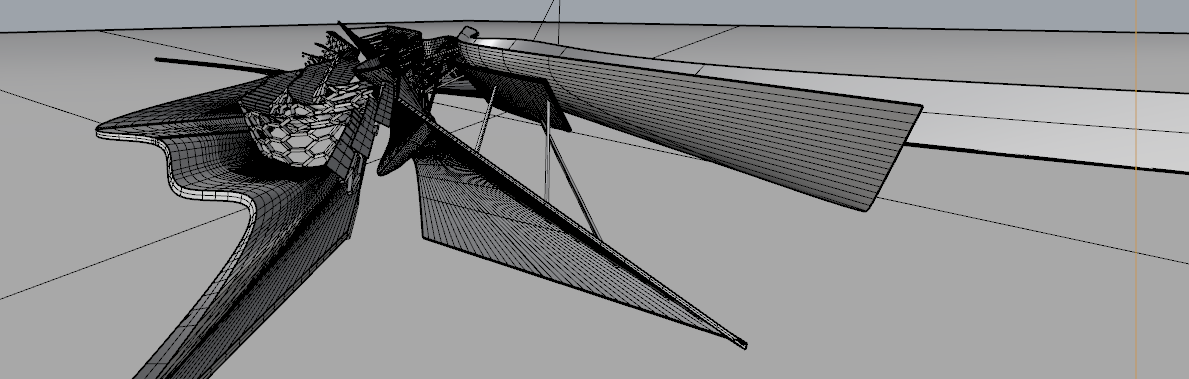
円弧近似って何?一体どうやるの?というと思うかもしれないので、実際にこの形状を設計者が提示してきた体で円弧近似をやってみます。
ところでなぜ、円弧近似を行うのでしょうか。並立断面に寸法を入れるだけではいけないのでしょうか。
実際に平立断面図を出してみてみましょう。
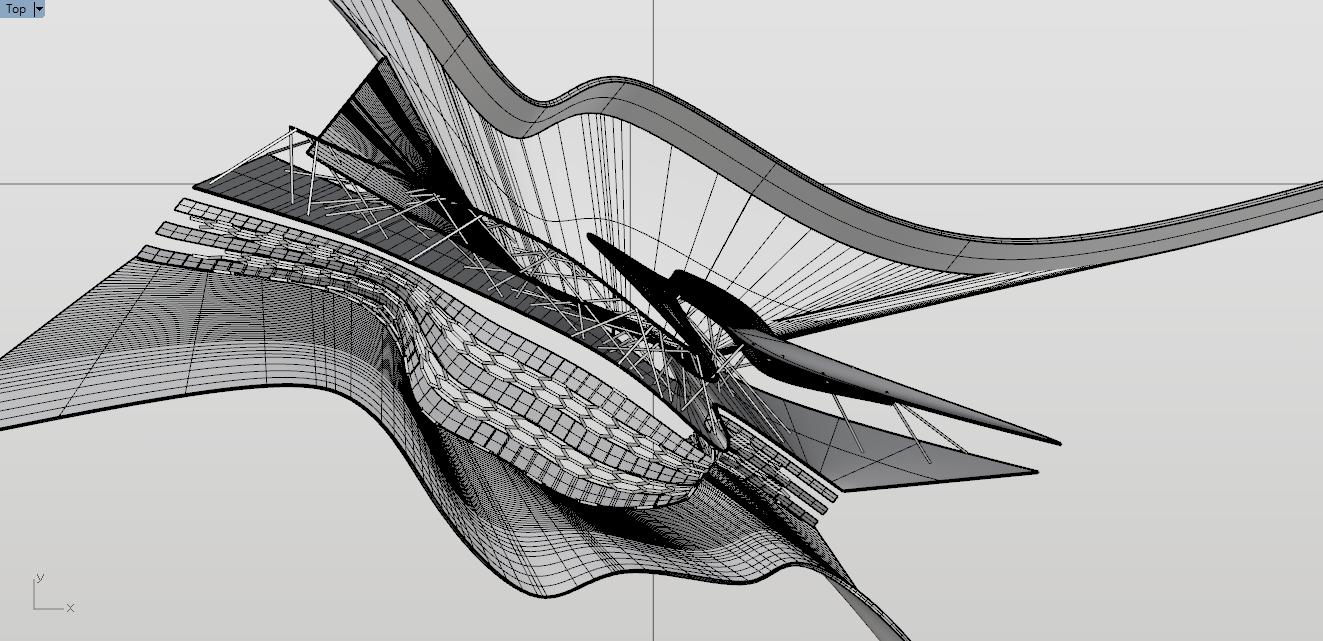
これが平面図になりますね。もうこの時点で、どこの寸法を追っていいのかわかりません。
平行寸法では測り切れないということが分かります。

次に立面図を見てみましょう。お?意外と普通だなと思ったと思います。
そうなんです。そんなに難しい形ではないのですねこれは。
3次元に展開しているとはいえ、平たい部分がかなりあります。
縦方向は平行寸法が有効なところもありそうですね。
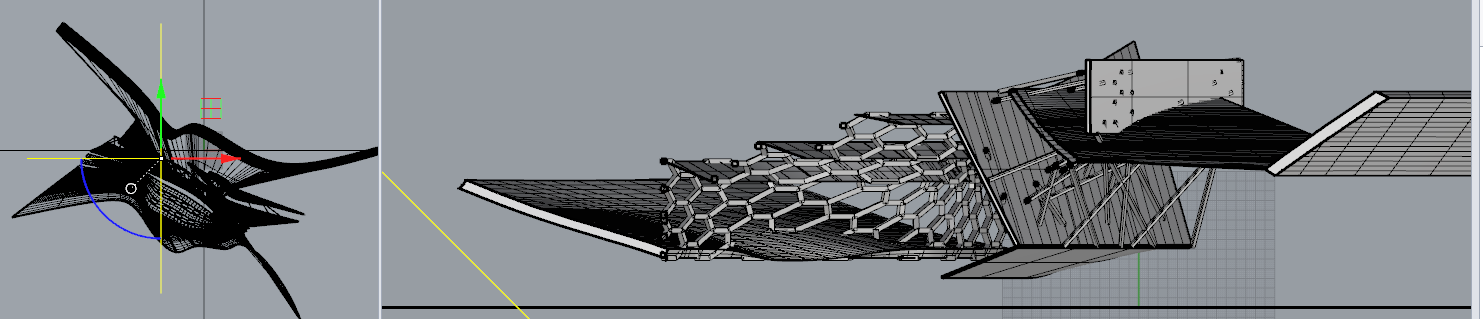
しかし、断面図を見ると、これは一筋縄ではいかなさそうだなという気もしてきますでしょうか。
この各ラインを定義してあげるにはどうすればいいかというのを考えていきたいと思います。
Grasshopperによる円弧近似
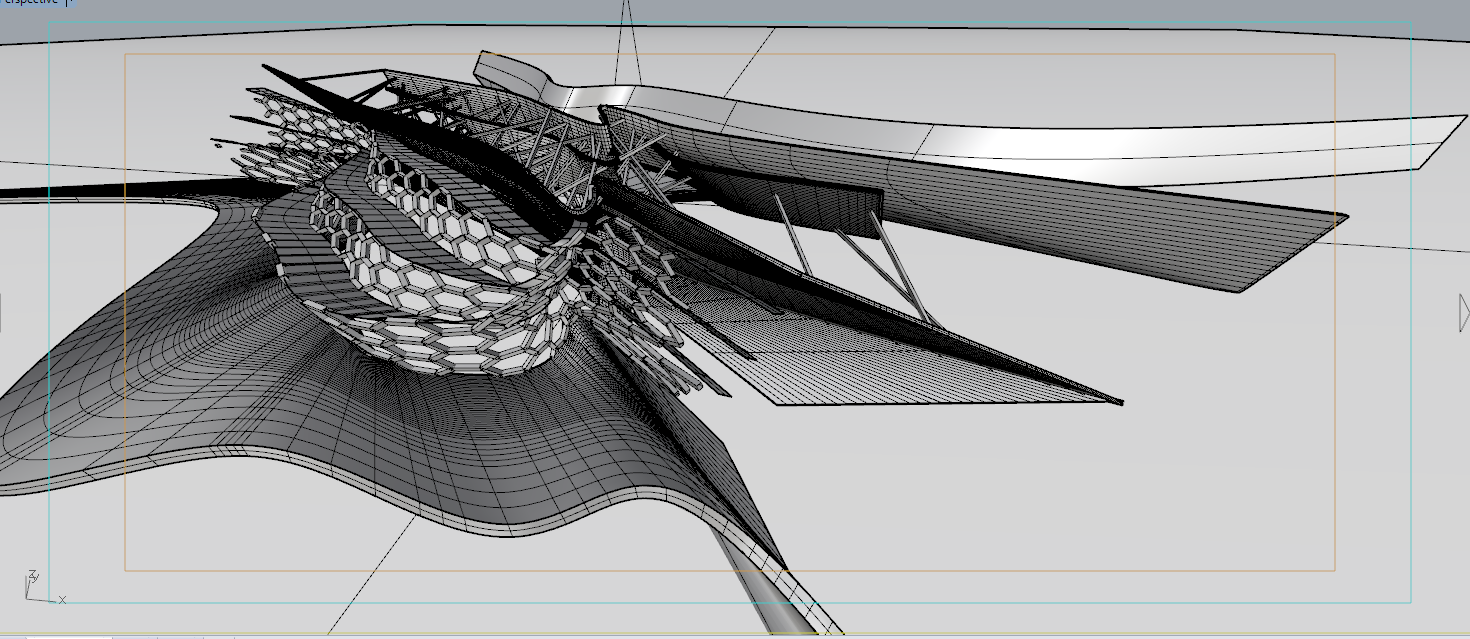
このモデルは適当に作っているので、円弧近似以前の問題で形の整理ができていないのですね。
そこで、まずはこのぐちゃぐちゃな形をまず読み取れる建築的形状へと綺麗にしてあげる必要がありそうですが、それは次章でやるとして、簡単な円弧近似をやってみます。
ここでやっとGHが出てきます。
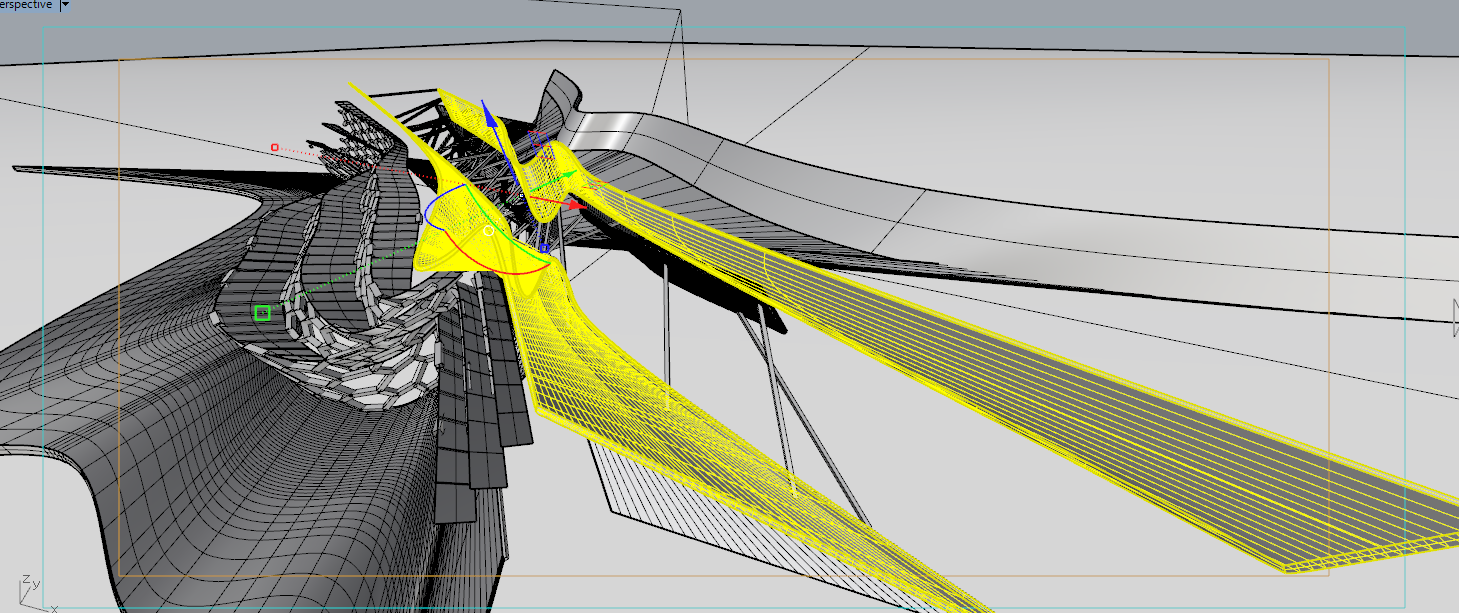
まずはこの二枚の板がデザインの骨になっているように感じるので、この二枚の板を分解して重要なラインを抽出します。
この二枚の板はポリサーフェスでできているのでBREPとして拾います。
そしてDeconstructBREPをかませます。
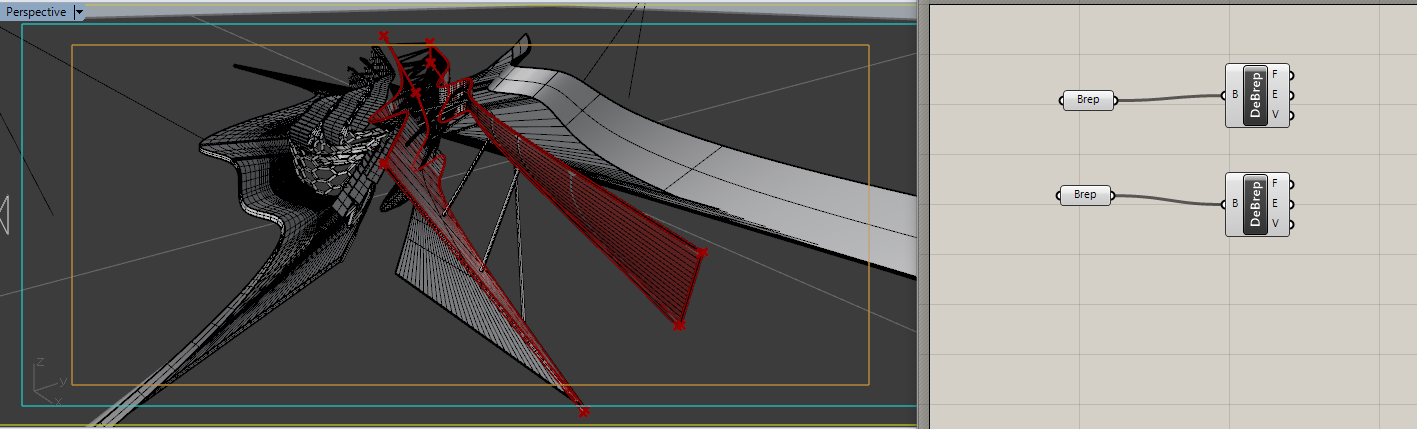
すると、FACEとEDGEとVERTEXに分解してそれぞれをツリー構造に入れてくれるので、ListItemsで拾います。
何番にお目当ての面が入っているかは実際にカーブを抽出して目視で確かめます。
抽出したカーブをReparameterize して、0~1のt値によって線が表せられるようにしておきます。
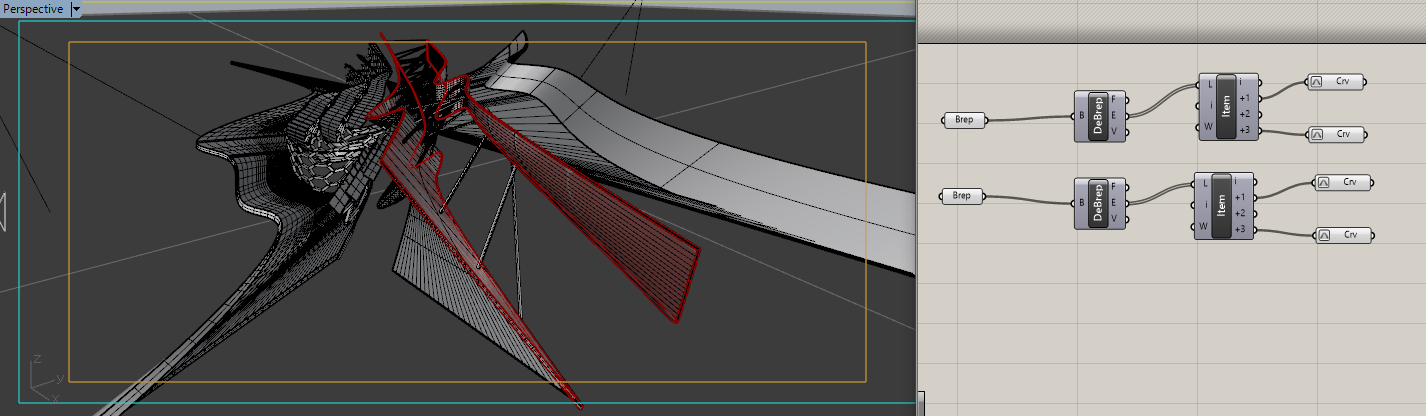
これで、EvaluateCurveをかけた時に、t値を0~1の範囲ですべてのカーブ上のポイントを表すことができることを確認します。
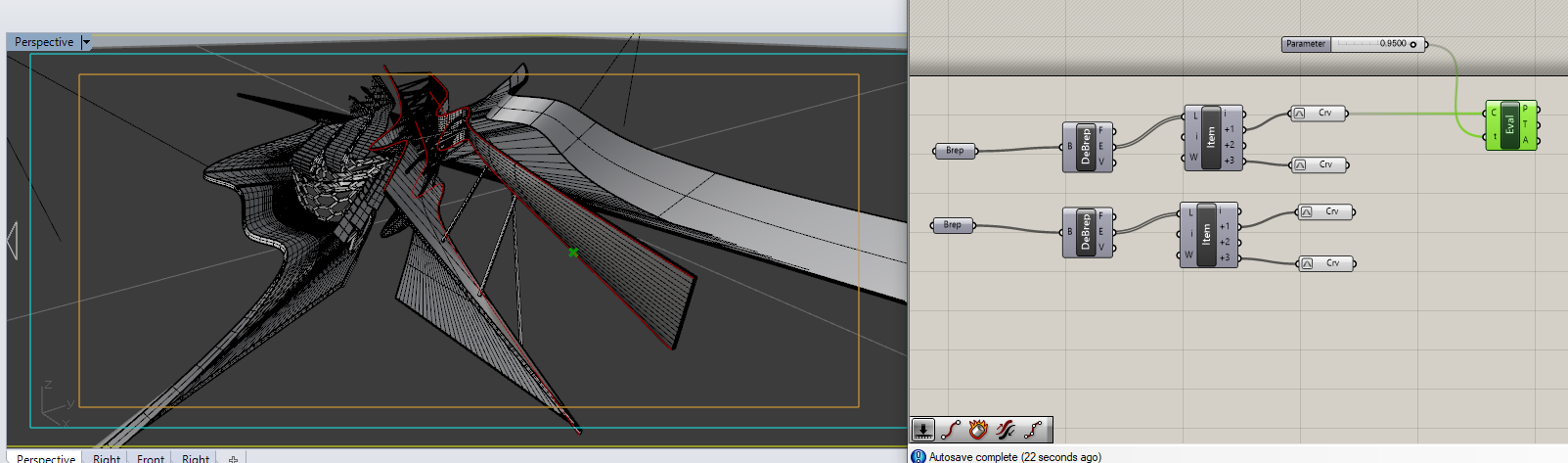
BiArchを使って円弧を2つに分割します。
先ほどのEvaluateCurveで端点を定義した時に、分割する割合を0~1で指定して二つの円弧で曲線を表してみます。
もちろん二つの円弧では十分細かくないことが分かります。
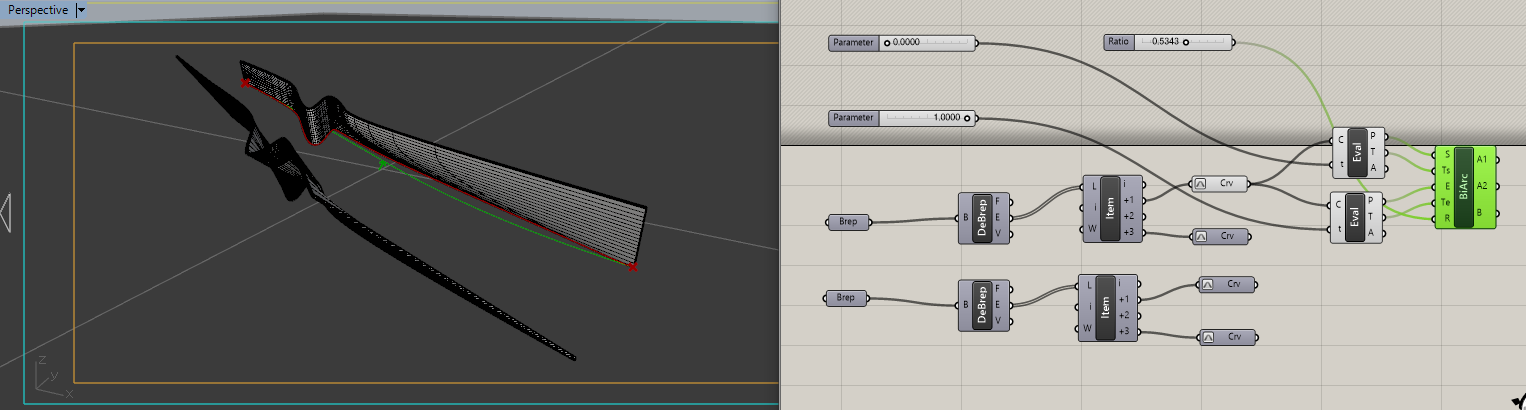
実際の形状に十分に近い変化を捉えるならば下の図の程度細かくないといけません。
EvaluateCurveのt値によって十分に近い距離のカーブを取った後、それをBiArchで二つの円弧で表し、CurveGraphで円弧のキツさをグラフィカルに表示します。
紫色の部分ではBiArchでできたそれぞれの円弧をDeconstructArcで平面と半径と角度に分解しています。
そして、中心点、円、中心点と円弧のエンドポイント(端点)をつなぐ線で表しています。
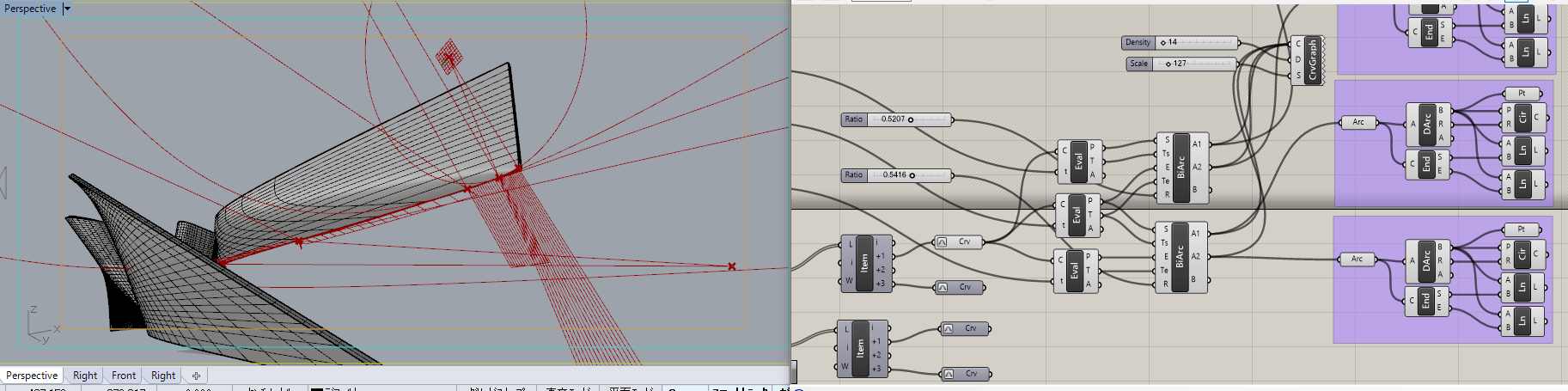
この時、曲線が同平面にないということがわかりますね。
この円の中心座標と、半径、それから、円弧のエンドポイント(両端点)を得られれば、この円弧を特定できる情報が得られたといえます。
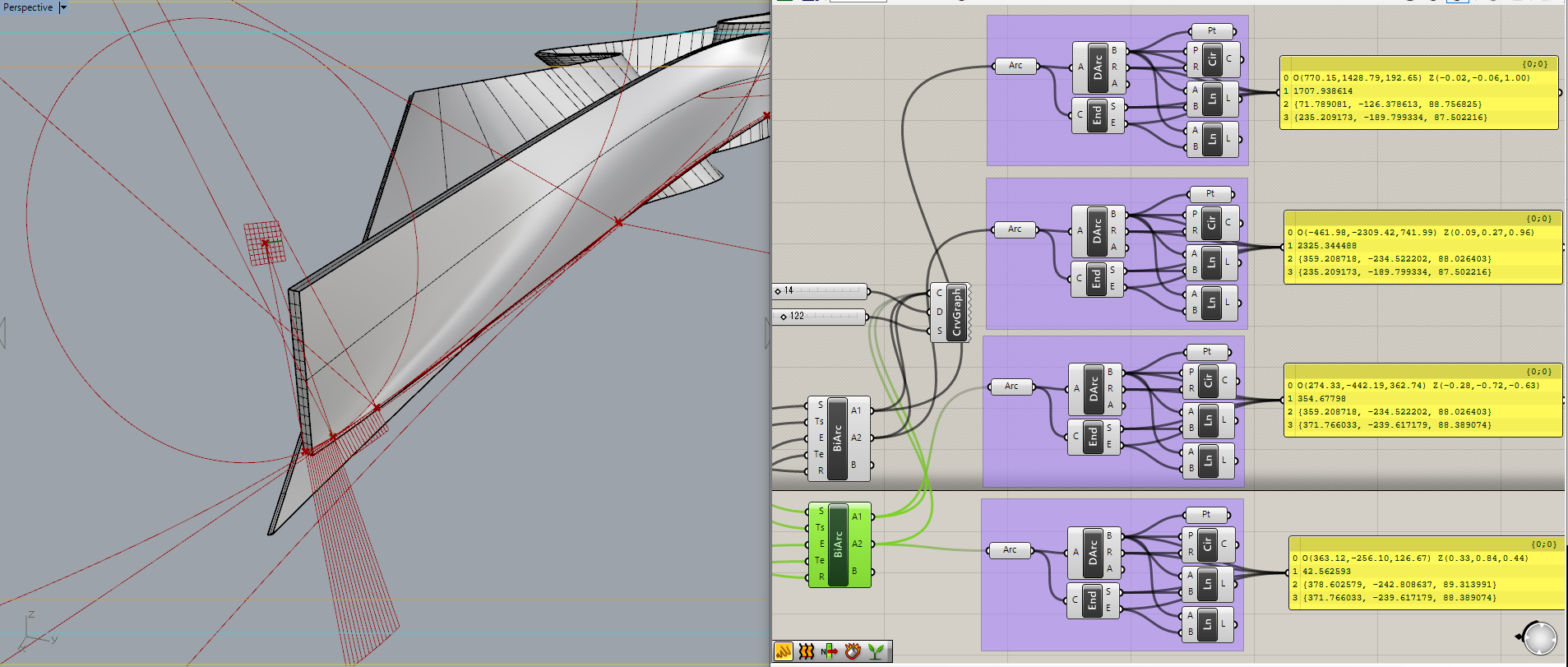
全体を振り返ると、お目当てのカーブを抽出し、EvaluateCurveで任意のt値でカーブを分割し、それをBiArchで円弧にさらに分解し、その円弧の情報を取り出してあげるという流れになります。
曲線のきつい所はより細かく割って表すことになると思うのですが、このプロセスが繰り返されるだけなので、実際に全部はやりません。
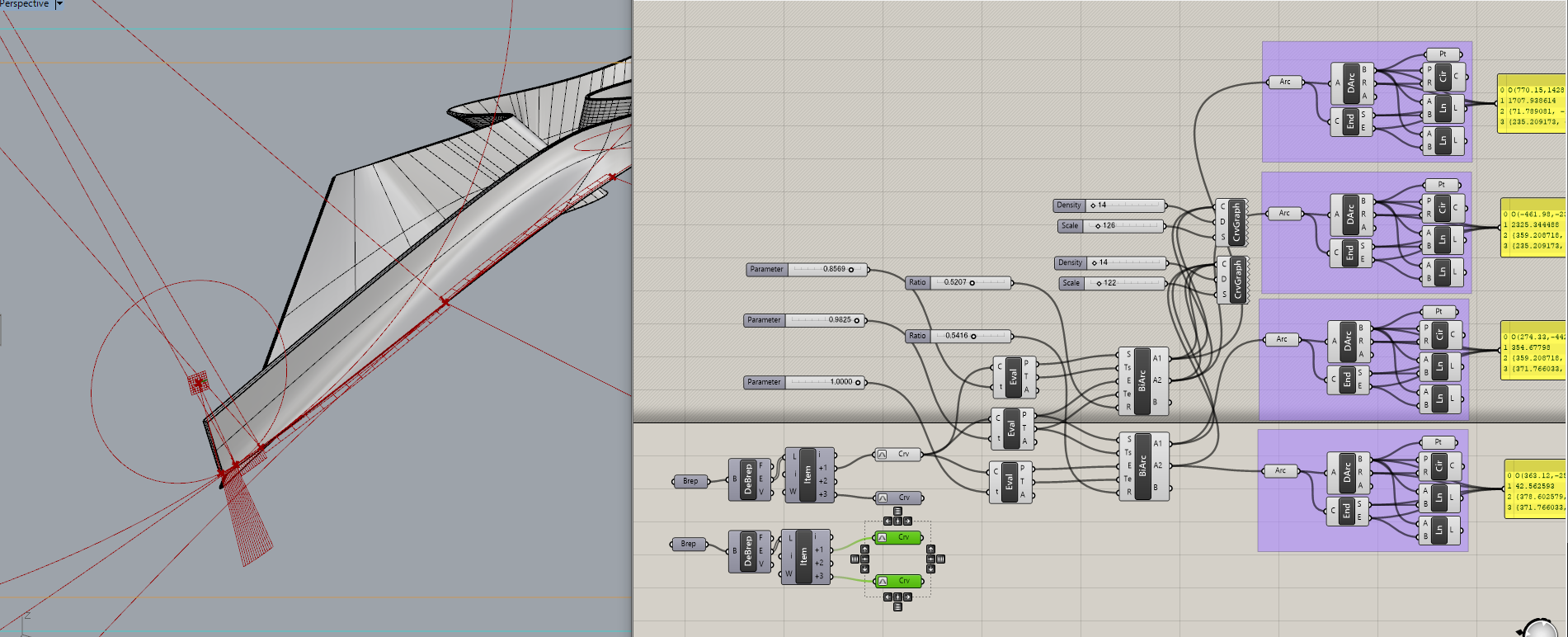
上のカーブも同様に拾ってあげることで、面を特定し定義することができます。
部分的にしかやっていませんが、ここまでで再現性がある情報の書き出しができる仕組みについてヒントが得られるのではないかと思います。
Grasshopperによる直線的メンバの情報抽出
逆に、3次元上にばらまかれた直線的な大量のメンバの情報を得たい場合はどうすればいいでしょうか。
例えば、先ほどの二つの壁に挟まれたメンバすべての情報を書き出すにはどうすれば良いか考えてみます。
このメッシュたちは32個の頂点を持ち、8つのFaceによって作られているようです。
これはどういうわけでしょうか。
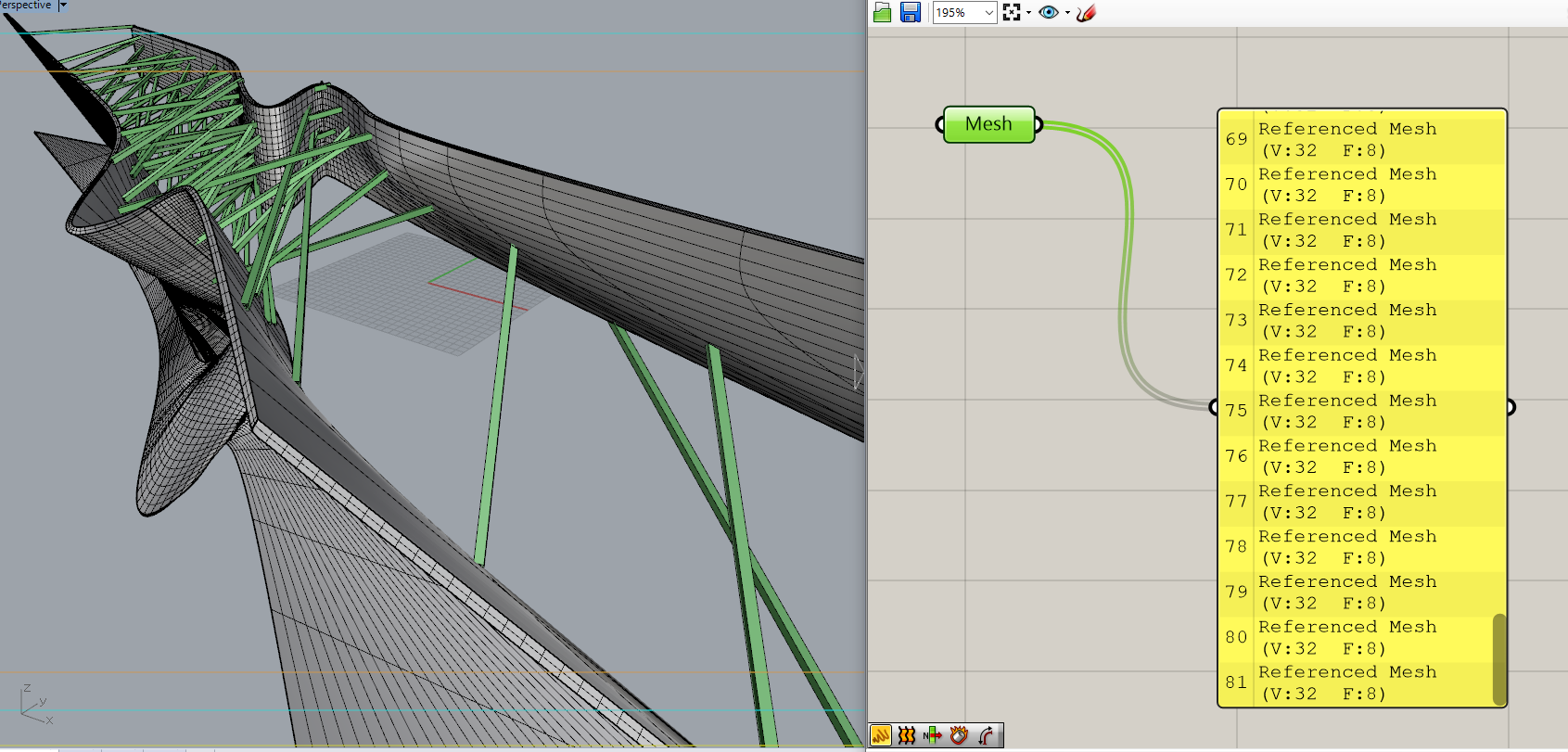
寄ってみると、なんとチューブでできているということが分かりました。
非常にめんどくさいパターンですね。
このメッシュの情報から、中心線、太さ、厚みを出してあげる必要がありそうです。
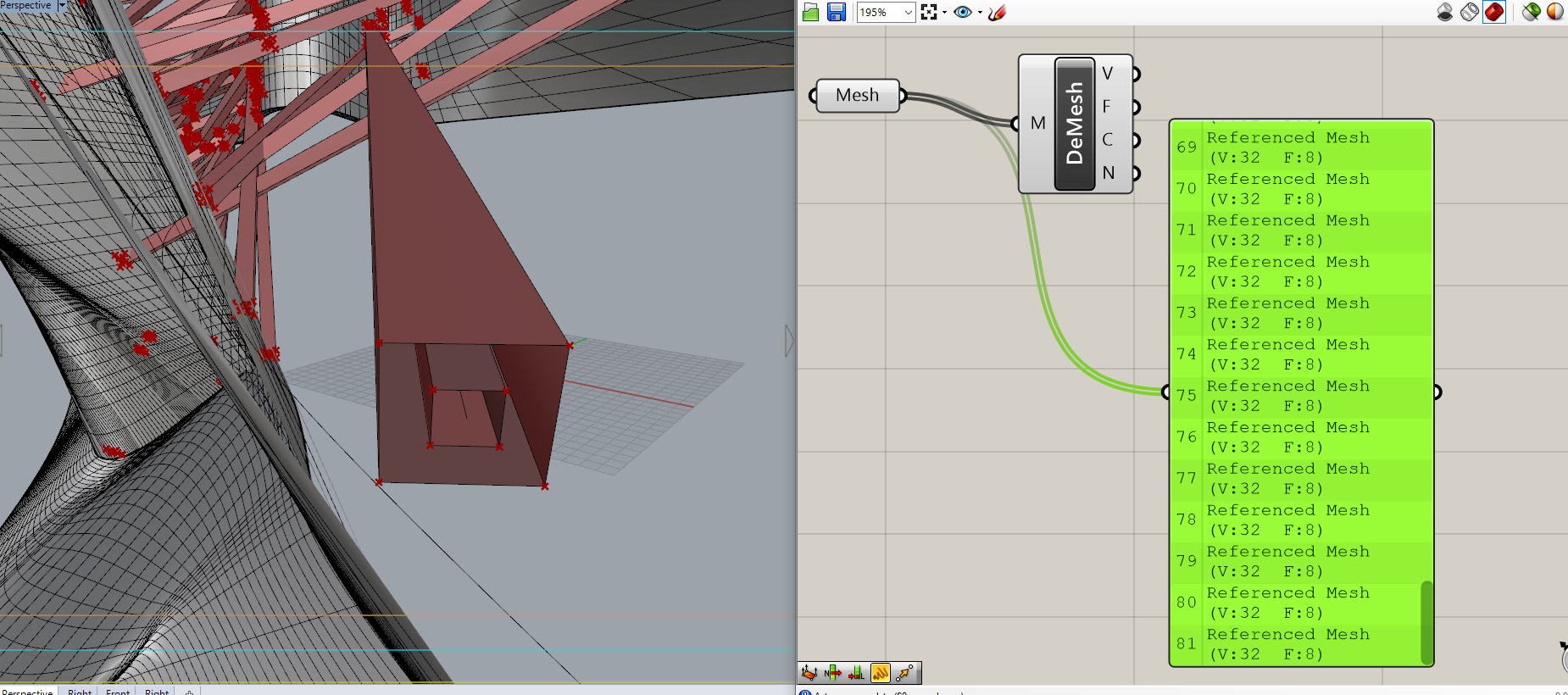
これにはいろいろとやり方があると思いますが、行き当たりばったりの計算方法で出そうと思います。
まずはメッシュのオープンエッジだけを拾います。オープンエッジというのは二つのメッシュに共有されていないメッシュのエッジのことです。
NakedEdgeとも表現できるかもしれません。
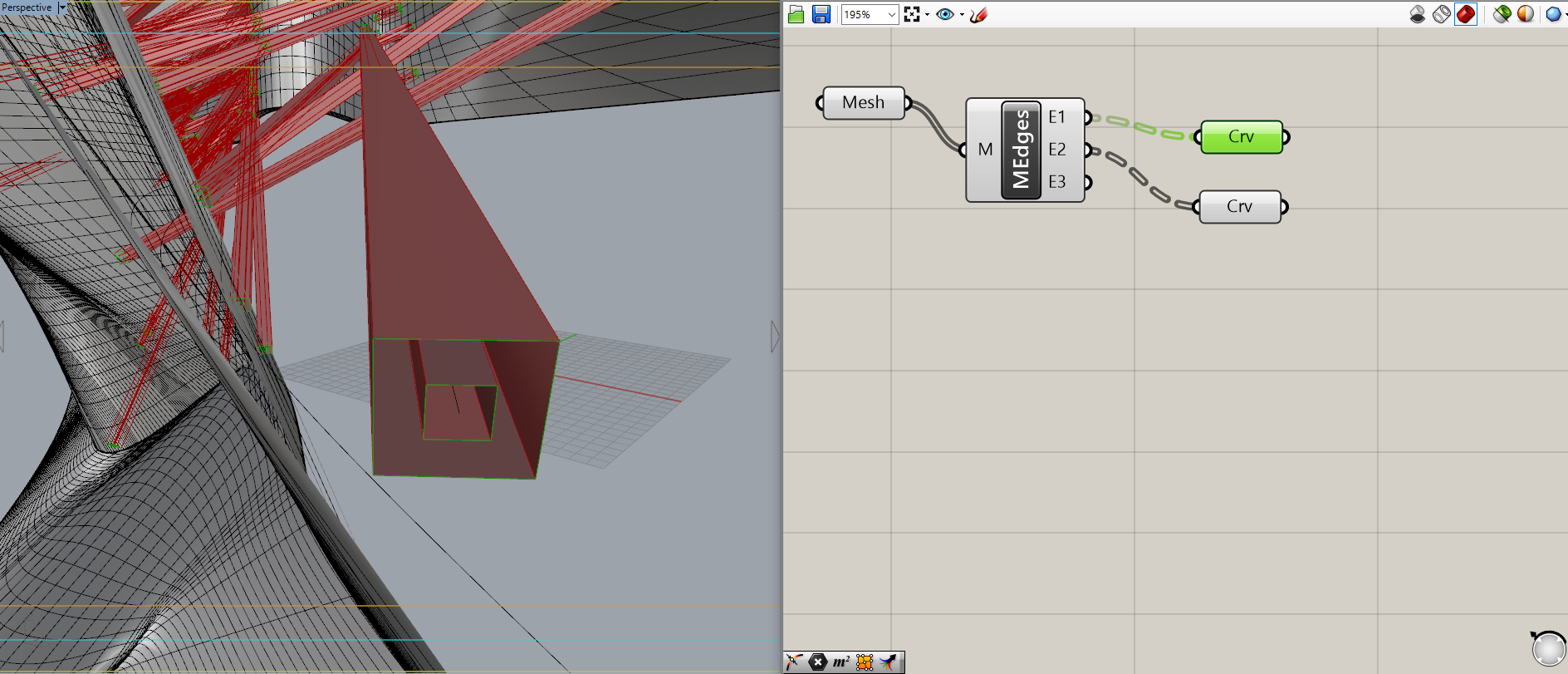
MeshEdgesというコンポーネントを使ってE1(オープンエッジ)とE2(クローズドエッジ)に分けます。
作戦としては、このオープンエッジをJoinCurveして4つの四角形を抽出した後、その四角形の線分の長さによってフィルタリングしようというものです。
現状、下の図ではJoinCurveによって両端の2重カーブが4つ拾われ、その長さがLengthによって表示されています。
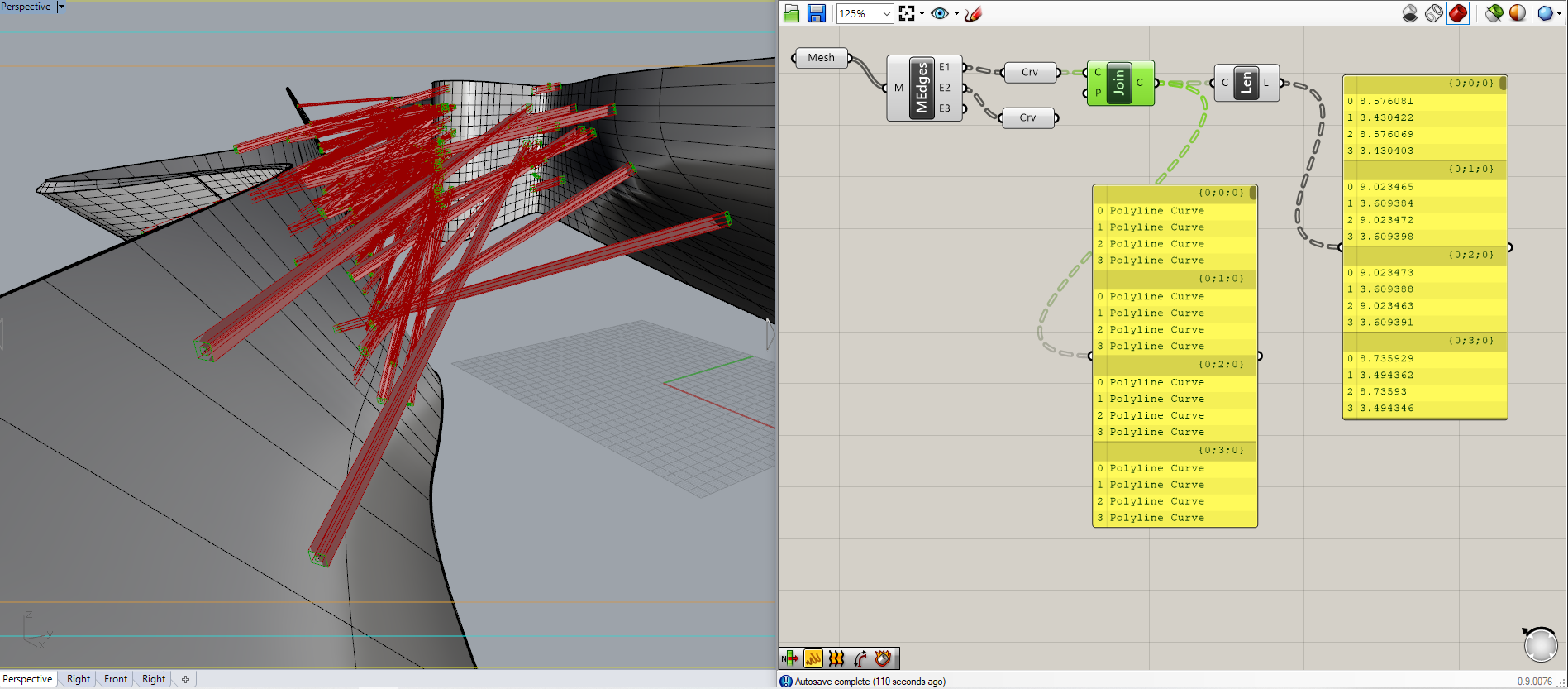
それでは、これを内側のカーブと外側のカーブに分類し、さらに同じ側にある端点の物とペアにする必要があります。
そのためにはまずはカーブをSortして、順序良く並べてあげ、短い方から二つ選べば、内側のカーブと外側のカーブを別々に拾うことができます。
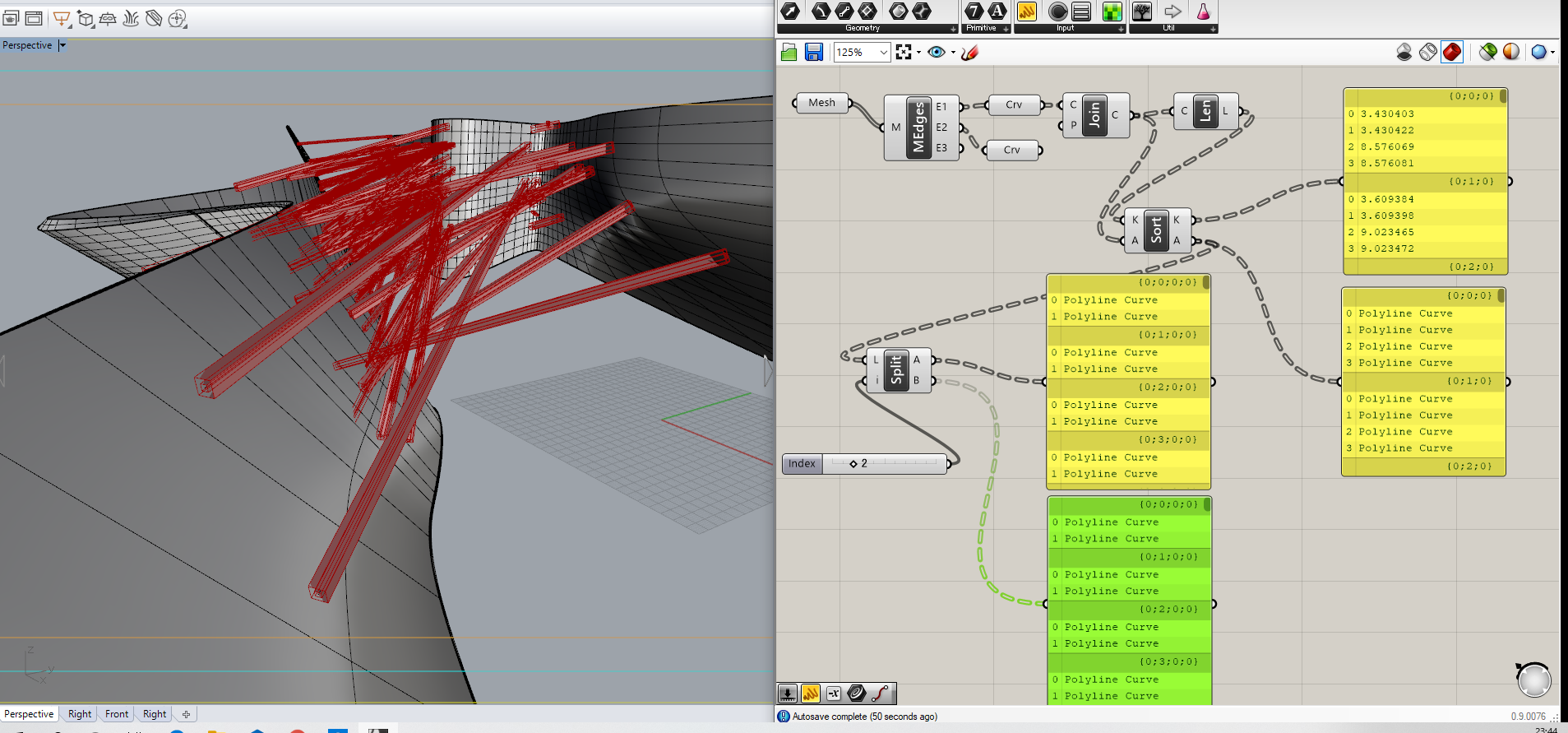
SortコンポーネントのKeyValueに長さLengthをつなぎ、Aにソートしたいカーブを入れると、小さい順にカーブがリストの中で並びます。
このリストをItemNumberの2番でSplitしてあげることで、外周のカーブと内側のカーブに分類することができました。
これをさらにどちら側のカーブなのか特定する必要があります。同じ側の端点と別側の端点に分けてあげないといけません。
そこで、中心点が一致しているかどうかで振り分けることにします。
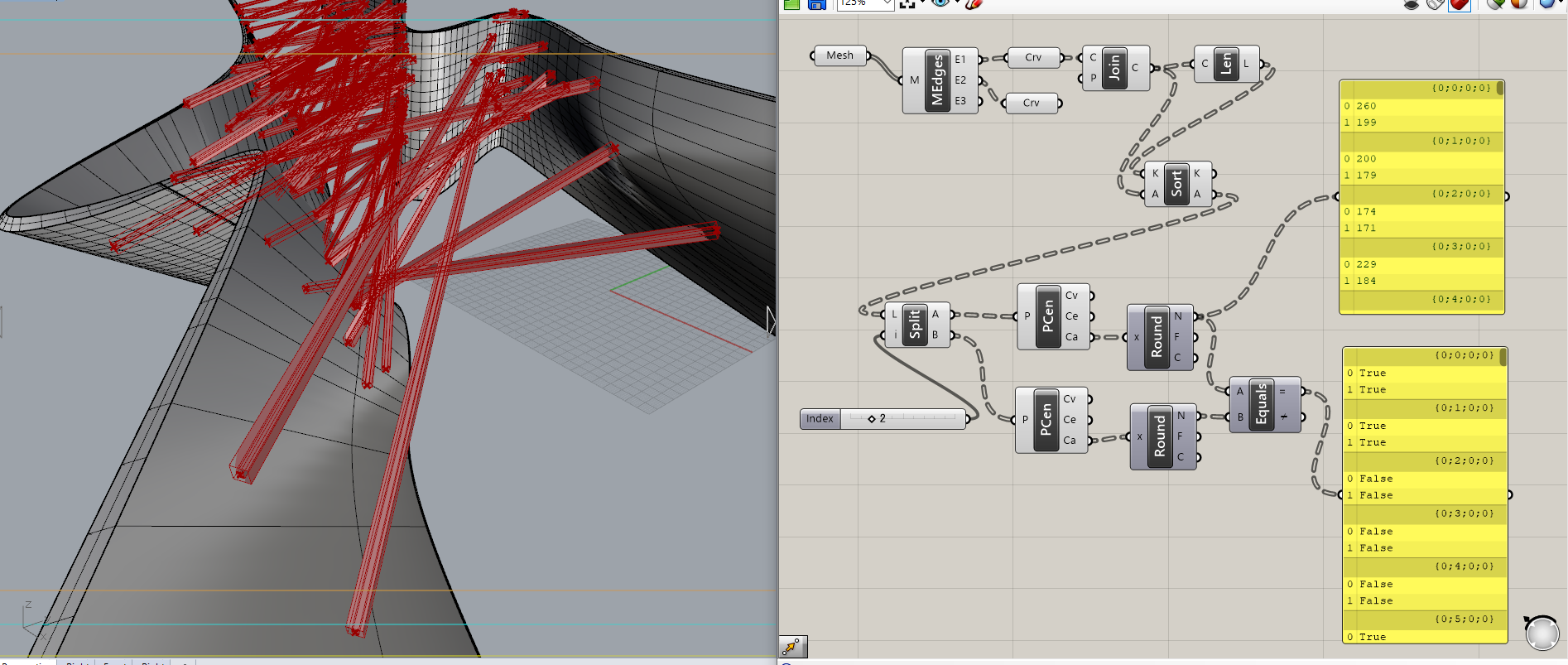
PolygonCenterコンポーネントで中心座標を書き出し、誤差をなくすために四捨五入Roundを使います。
0番と1番に入っている外周のカーブデータが、0番と1番の内側のカーブと順序が一致している場合のみTrueを返し、一致してない場合、Falseが返ってくるようにEqualityコンポーネントでBooleanの値を確認します。
ということは、Falseが返ってきている物はリストの順番を入れ替える必要がありますね。
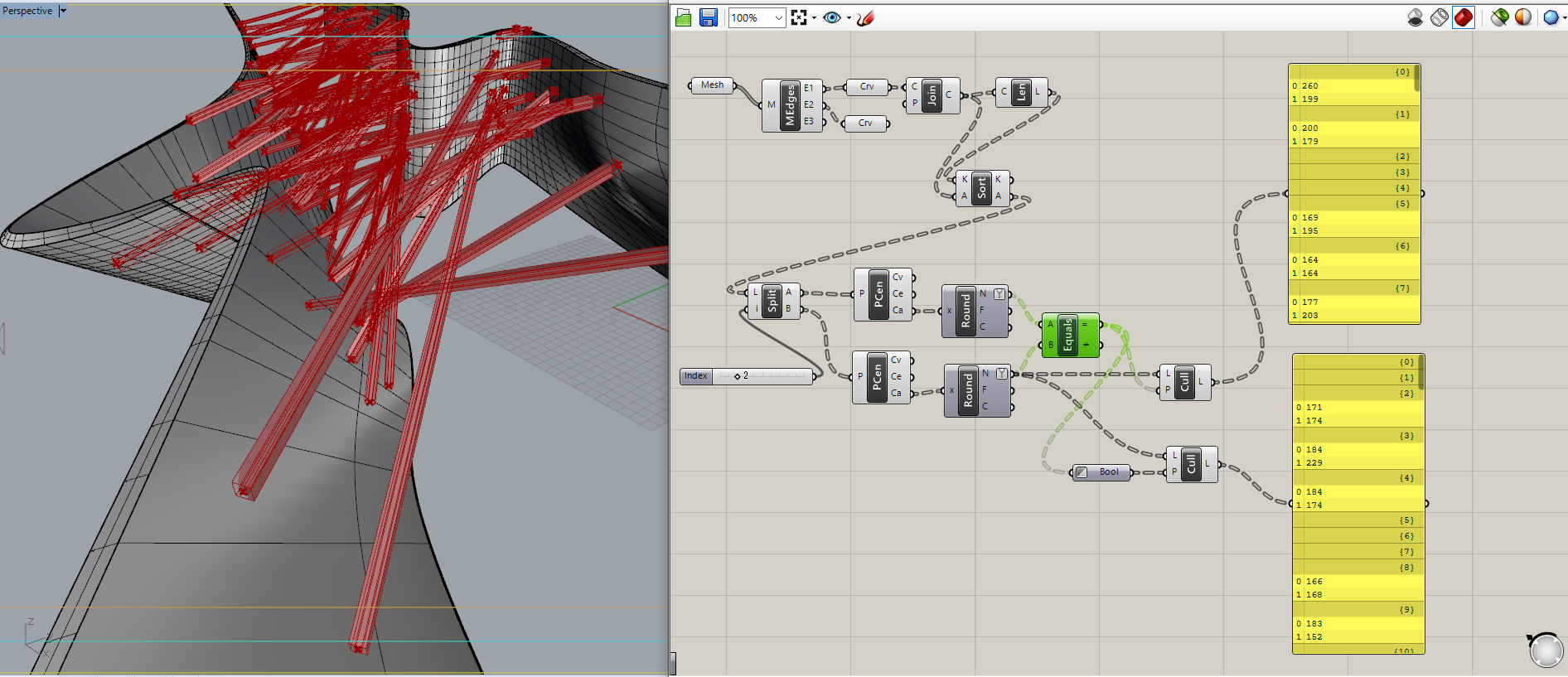
CullPatternによって、順序が正しいリストと、BooleanのInverse(true falseを入れ替えたもの)を使ったそれと順序が逆のリストを分類します。
これによって下のリストだけをReverseして上の正しいリストとMergeしてあげれば、全ての向きが揃うことになります。
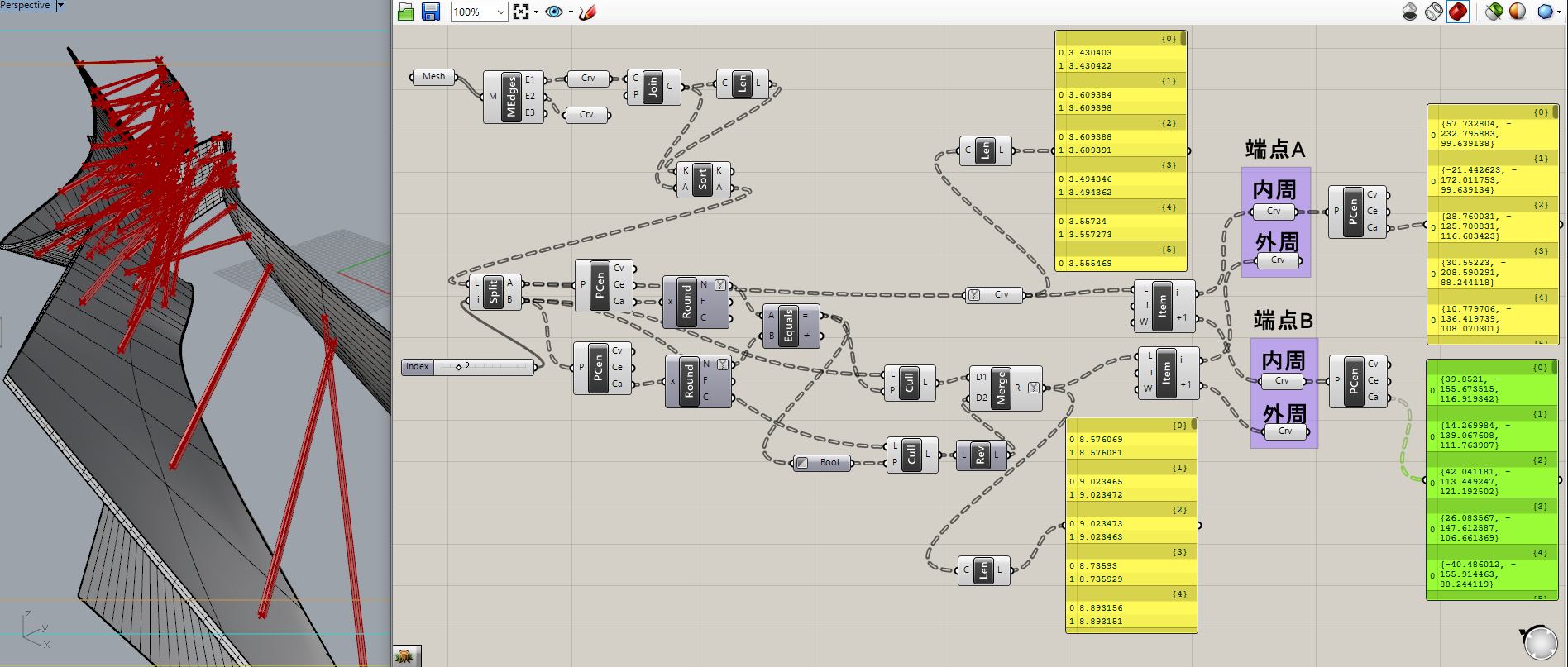
これで端点A、端点Bそれぞれの内周と外周にカーブが分類できたので、中心点を拾うことでメンバの端部の座表情報を得ることができ、かつ内周と外周のデータから簡単に太さ、厚みを逆算することができます。
このようにしてGHで簡単にメンバのデータを自動で整理し、出力することができます。
これによって再現性のあるメンバのデータが作成できることになります。
次は、複雑な部分をどのようにラショナライズして、安く作れるようにするかということについて考えます。
施工者が複雑な造形物を作る上でどうやったら安く作れるか

まずは、パネリングのサイズが規定値を超えないか、複雑なカットがないか、曲げがあるか、曲げが1軸方向か2軸方向か、曲げ半径が決まっているか等でコストがガラッと変わってくるようです。
私はファブリケーションサイドで検討したことがないので、あまり詳しくはないのですが、金型がどうとか、曲げ半径の制約とかがあるということを聞いています。
シンプルな形状で標準化されればされるほど安くなるということはなんとなく理解しているつもりです。
要するにバリエーションに富んだ形であっても、分解すると同じパーツの繰り返しでできているみたいなことになれば安く作れる可能性が高いわけです。
これをどうするか考えるというのが実際にカッコいい変な形を実現できるかのポイントになってきます。
標準化・単純化によるデザインの変更
これは元の形状に忠実にやろうとするとかなり難しいので、ある程度の単純化は必要になってきます。
それが設計者にとって、そしてクライアントにとって、許容できる範囲内なのかというのがポイントで、施工者サイドから出てきた条件をもとに組み直された案を吟味することになります。
施工者って実はとてもすごい技術を持っていて、実際にファブリケーションするノウハウを持っているわけです。
設計者はどちらかというと、こういう形になったらいいなーみたいなフワッとしたノリ(?)で図面を書いたりしているので、あまり現実に即した問題解決がなされていない場合があります。
施工段階でそういった単純化を行う必要があるのであれば、逆に言えば施工サイドの納まりの必要前提条件ありきで、その範囲内で設計した方がうまくいくのではないかと思ったりすることもあります。
実際にカーテンウォール・コンサルタントが設計段階から参入していてパネルの割り付けについて詰めている場合もあると思います。
ただし、そのカーテンウォールコンサルタントが実際に作るわけではないので、結局は施工者とのすり合わせは別途必要になると考えています。
標準化・単純化の実例
それでは、実際の標準化単純化をやってみます。
上の形状についてできる部分は単純化して安く(たぶん)作れるようにしてみたいと思います。
具体的にどこが標準化できるでしょうか。
例えば、下の二つは確実にできる標準化になります。
標準化のポイント
- 1.2次元平面に展開できるデータを作成する事で平らなパネルで構成する
- 2.同じパーツの繰り返しによって金型を減らす。
この2ポイントについて、考えてみたいと思います。
2次元平面に展開できるデータを作成する
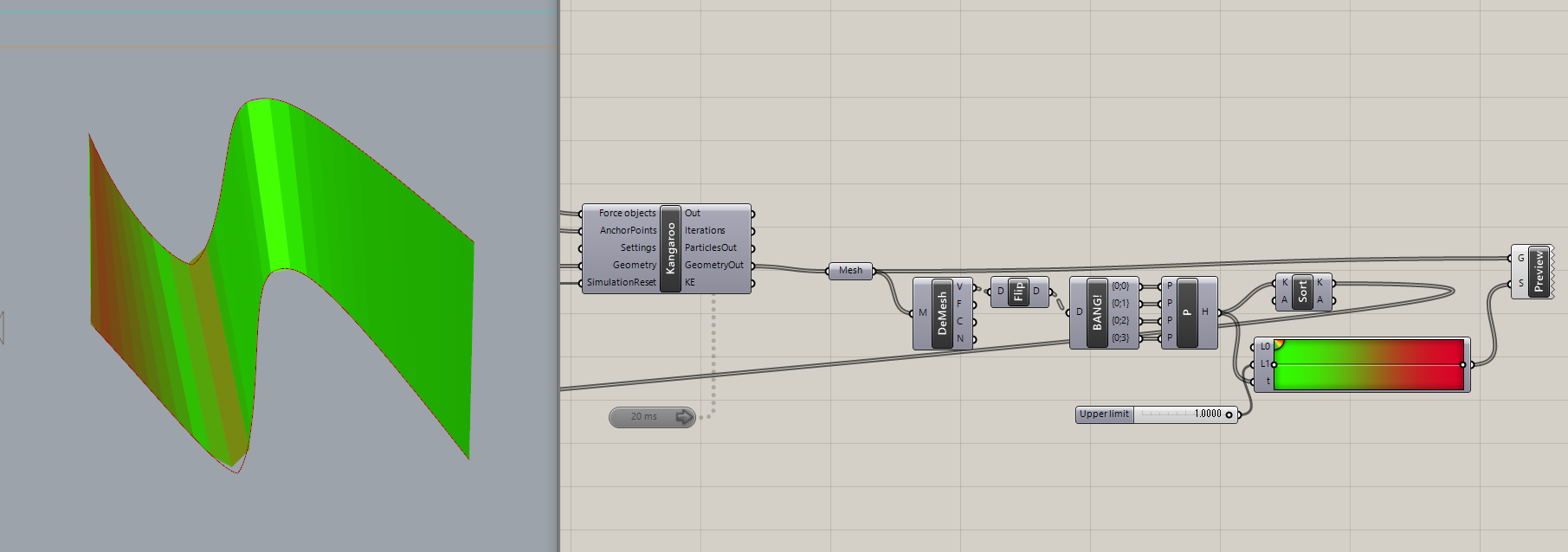
上の図は壁の一部分をKangarooで捻れがなくなるように力をかけて物理シミュレーションをしてみたものです。
Kangarooについては長くなるので需要があれば別記事で書こうと思います。
最適化を行った後でもまだ、赤い部分、捻りがある部分が残ってしまっているのが確認できます。
これは上のカーブと下のカーブが捻りの状態になっているために起こっていると考えられるのがまず一つ目の原因です。
それから、カーブがきつい部分ではジオメトリが整理されていないのが二つ目の原因として考えられるとおもいます。
そこで、捻れの場合と、きついカーブの処理を別々に考え、それぞれ処理していこうと思います。
捻れが起きている場合にどうするか
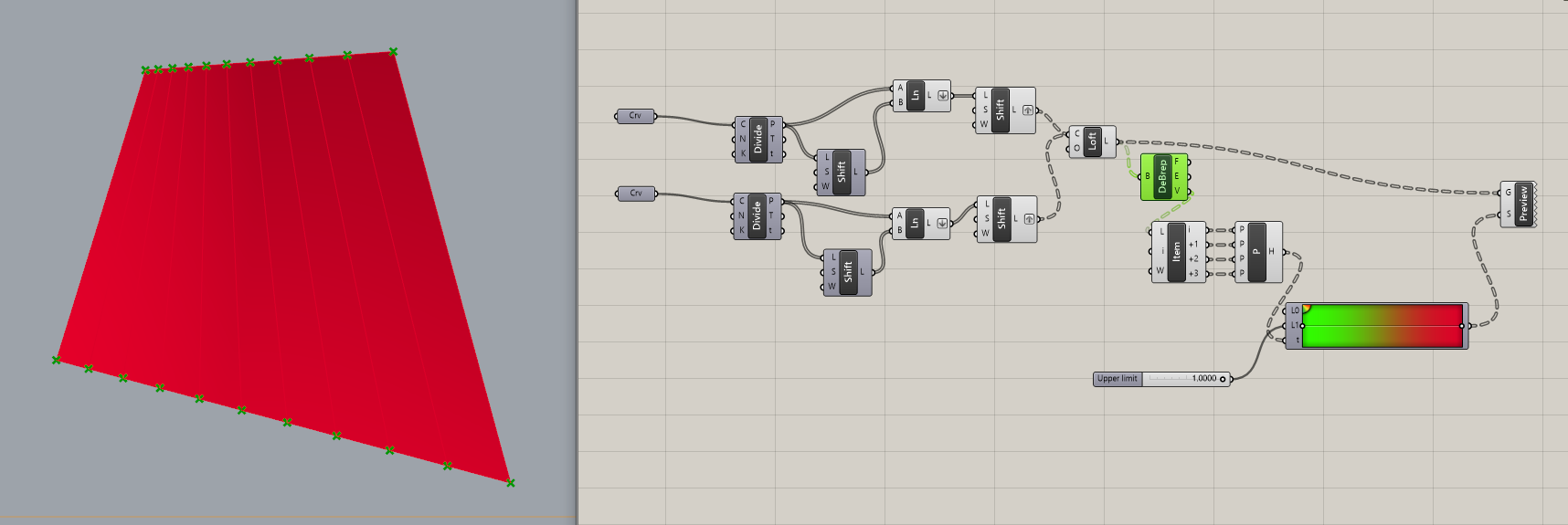
これは単純な直線のねじれが起きている場合に状態を限定して考えます。
今現状上のカーブと下のカーブをDivideCurveしてあげて、ShiftListで隣同士の点をLineでつなぎ、上の線分と下の線分をロフトしてあげたところです。
Planarity(捻れ)を確認すると真っ赤になっていることが分かります。
これは捻れが強いということですね。それではこの捻れを解消してあげるにはどうすれば良いでしょうか。
一つは3角形を作ってしまうということが考えられます。
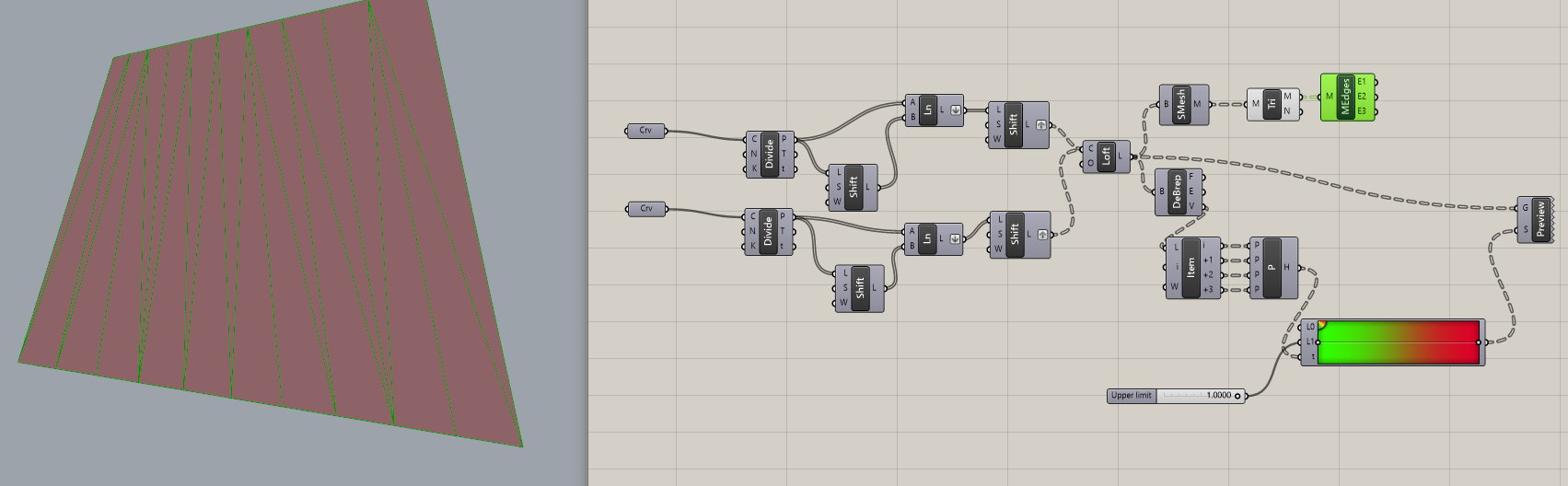 SurfaceをSimpleMeshでMeshにして、Triangulateで三角形に分割します。
SurfaceをSimpleMeshでMeshにして、Triangulateで三角形に分割します。
MeshEdgesで分割された線を見てみると、当然三角形なので捻れはないということになります。
ただし、これでは鋭利な小さなパネルが出てきてしまいそうです。
ある程度の大きさのパネルで割ることはできないでしょうか。
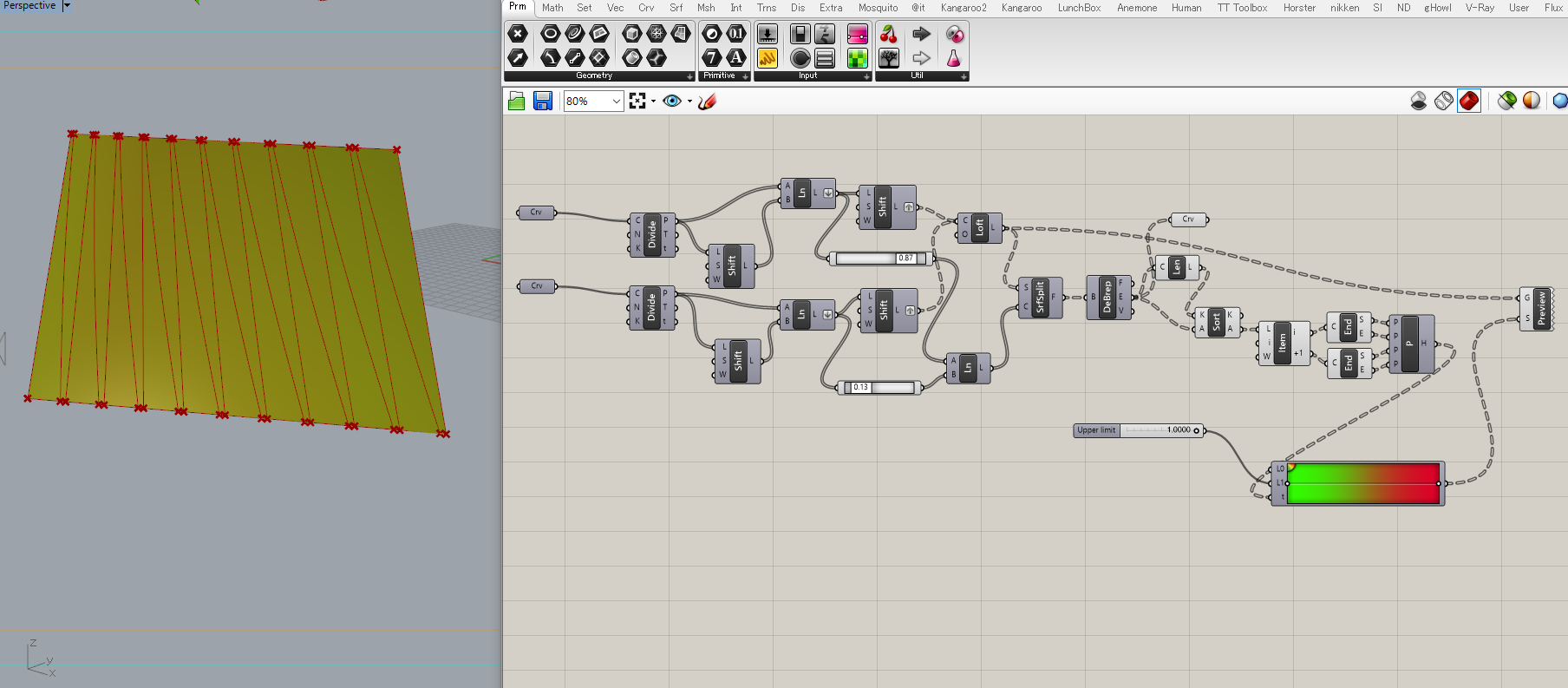
折衷案として、細いパネルが出てきてしまいますが、台形に割るという手があります。
この割り方であれば、少なくとも一様に捻れを分散させた状態でかつ、三角形を作らずにすみます。
しかも似たような形のパネルが沢山出てきていますね。
これを横方向に6分割にしてみましょう。
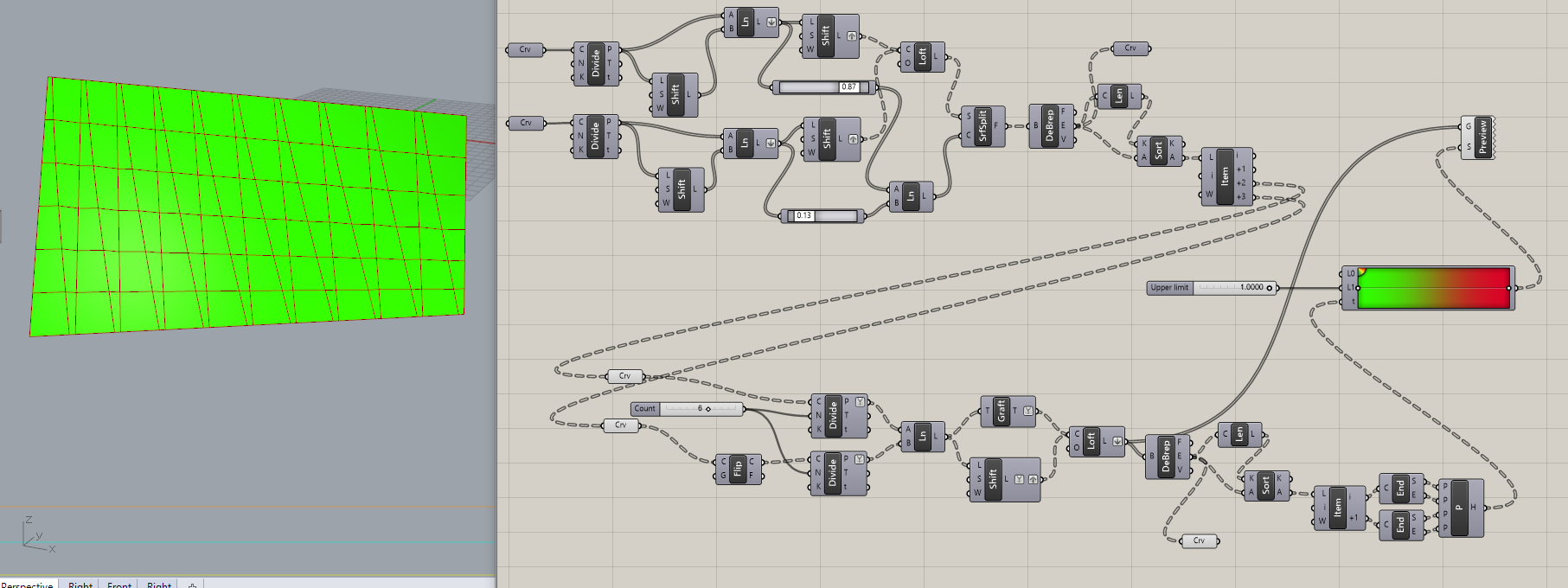
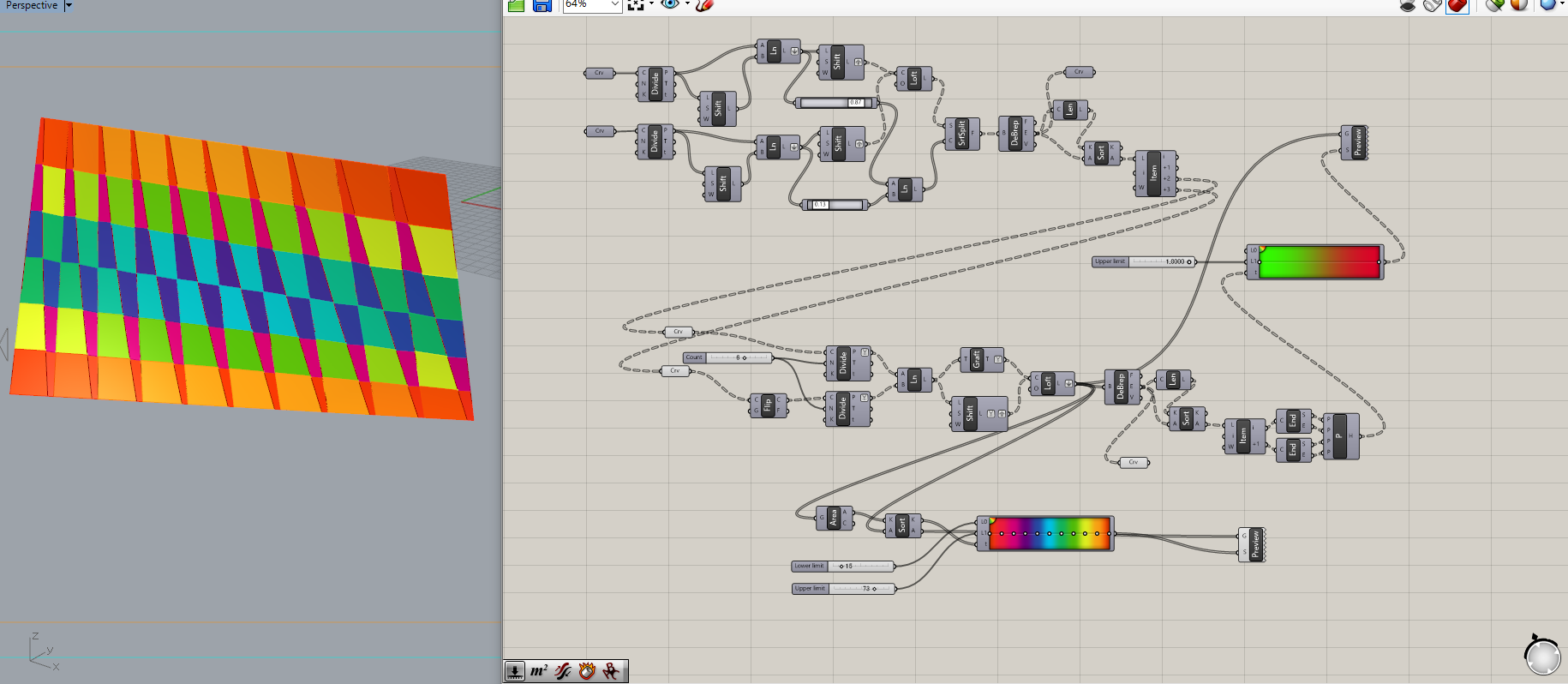
少しガタガタになってしまいましたが、概ね平らで、かつ相似形が沢山出来る形状に分割することができました。
面積によってフィルタリングしてあげると似たような形のパネルが沢山あることが見て分かります。
マリオンによって誤差を吸収させてあげることを考慮すれば、かなりの最適化が可能になると思います。
これであれば少ない枚数のパネル形状で捻れた面を構成してあることができそうです。
きついカーブ面の場合
きついカーブ面を構成する場合コーン(円錐)の部分のような形で近似できないか考えることが多いように思います。
円錐の部分であれば捻りなしで作ることが可能なのは想像がつくと思います。
では、先ほどのZ型のカーブをアバウトに近似してみます。
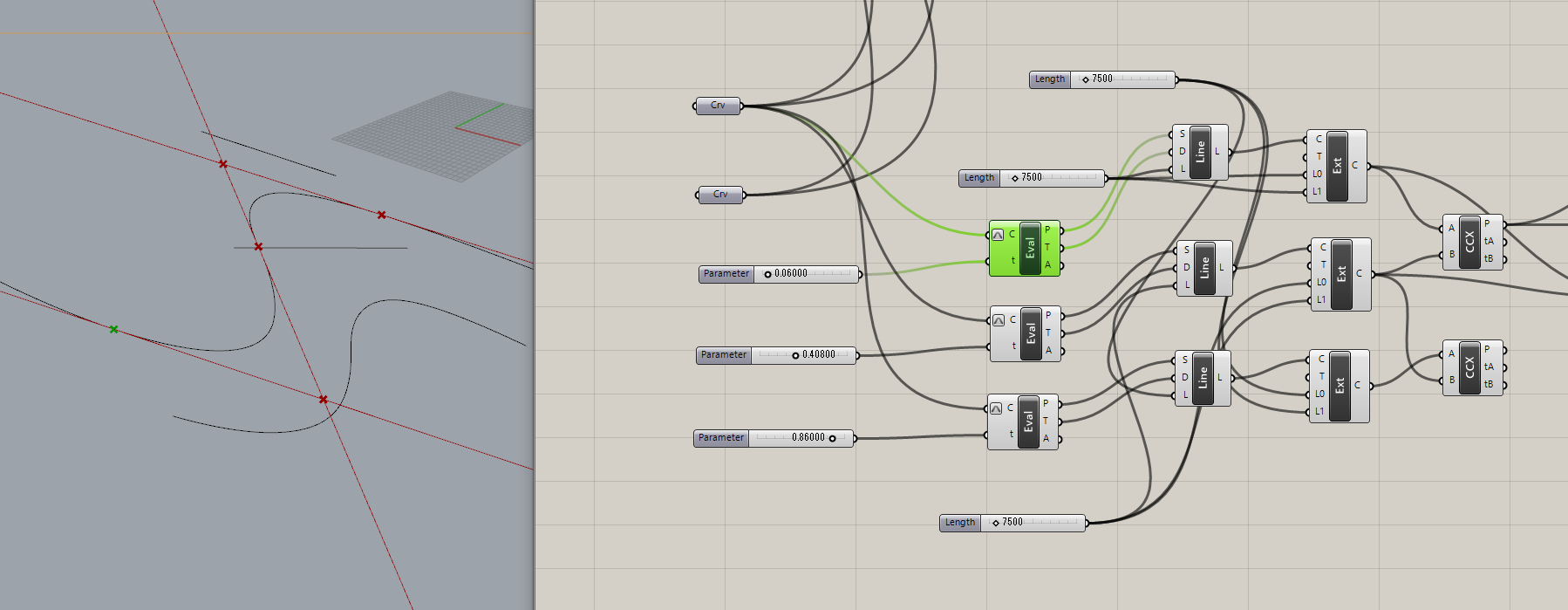
まずはReparametrizeした上辺のカーブを重要だと思う3点でEvaluateしてLineSDLで接線を出し、ExtendCurveで両方向に延長してCurveCurveで交点を計算して求めます。
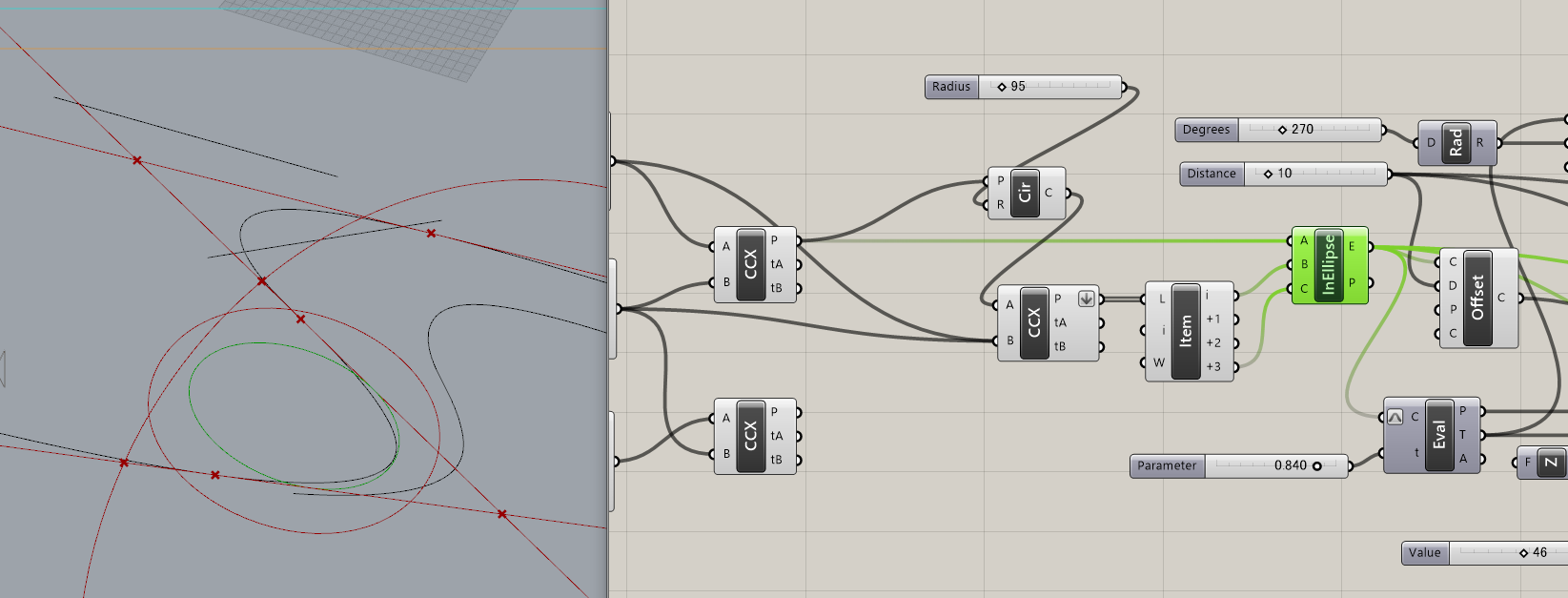
二本の接線に内接する楕円をInEllipseで出すために接線に対して円を書いて、大きさを合わせるための点を接線上に取ります。
二本の接線との交点と接線上の点2つの合計3つのポイントを用いて楕円を描きます。
そして、下辺のカーブを近似(?)した楕円のオフセットカーブを作成します。
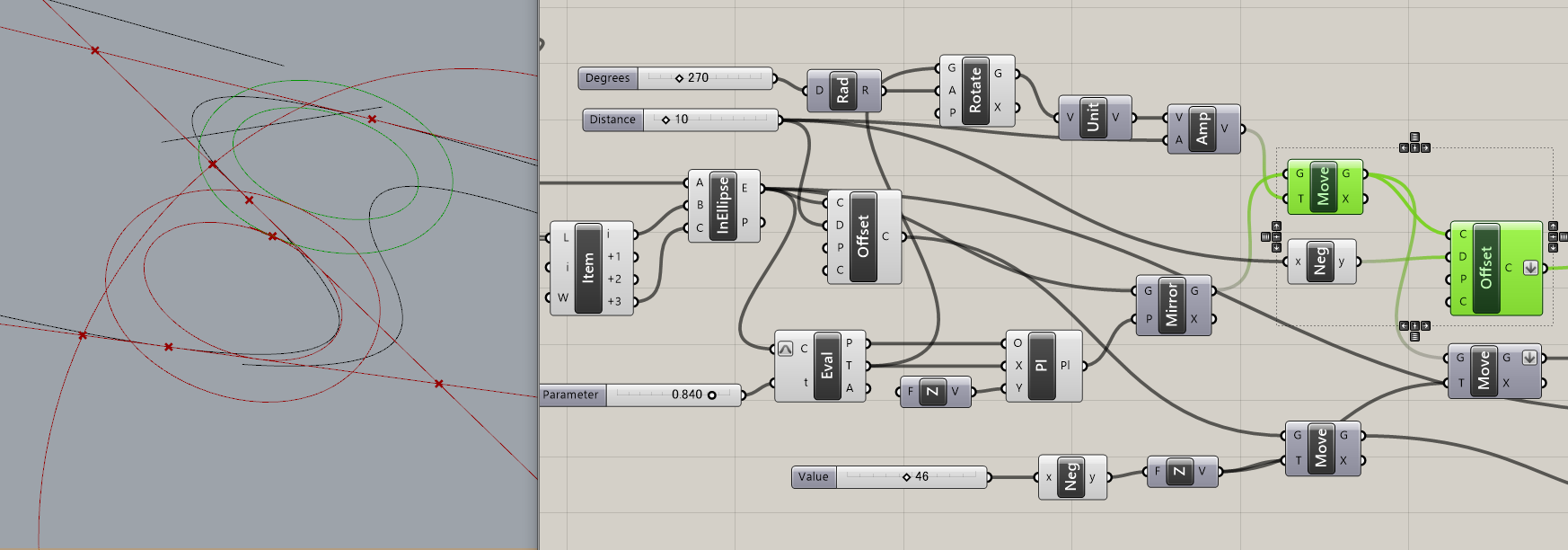
今回は安く作るために同じ大きさのコーンに似た形で近似することにします。
ここまで変えてしまうと近似と言っていいのかわかりませんね。
それから、これは厳密に言うと円錐の部分ではありません。
円錐の部分を等倍率で変形してもオフセットが一定になることはないと思いますので。
EvaluateCurveで丁度良い点を探して楕円をその接線とZ軸で構成される面に対してMirrorします。
そして、接線と直角の方向のベクトルを作成して、その方向にオフセットの分だけ移動します。
さらに、その楕円のオフセットを作成して、これで対になる二つのコーンのベースラインができました。
Z型のカーブを出すには、これからコーンを分割する必要があります。
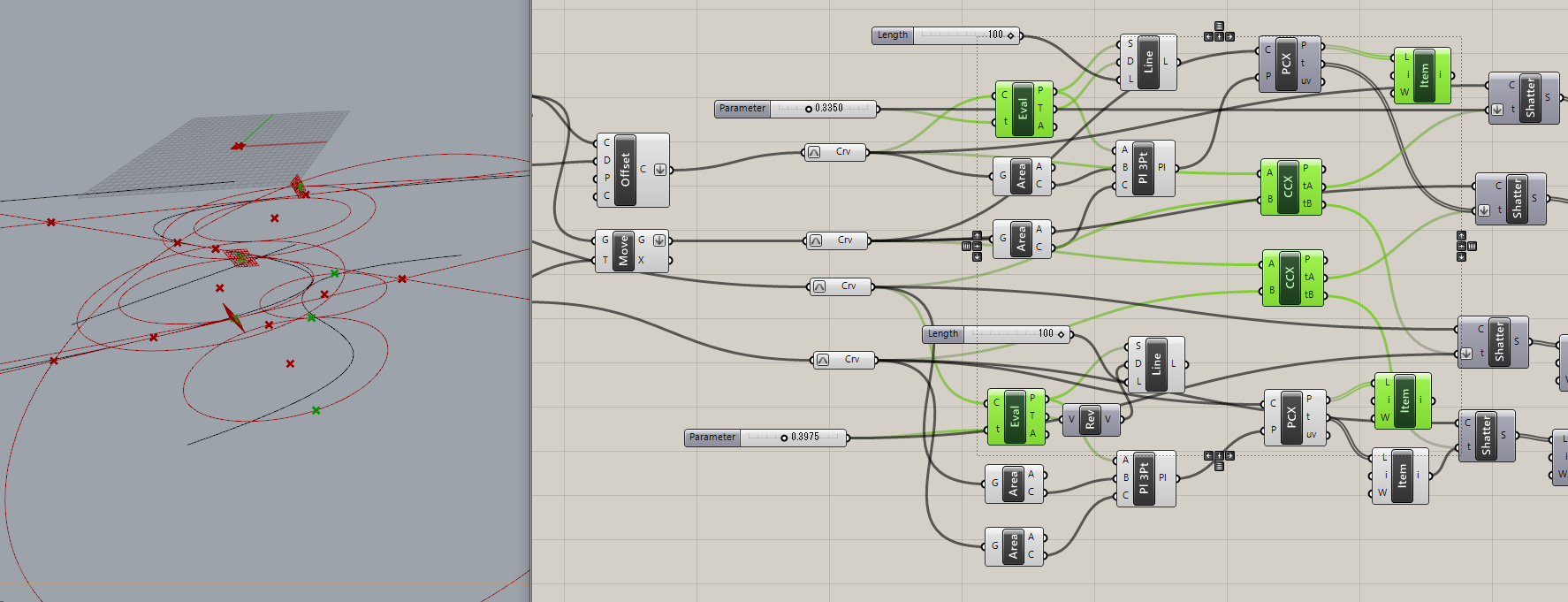
コーンを構成するカーブの交点と、壁がある側の接線を同じようにEvaluateCurveとLineSDLで求めます。
接点と楕円の中心線を通る平面で上下のカーブに同じような場所に分割点を作成します。
それと同時に、楕円と楕円の接点もCurveCurveで求めておきます。
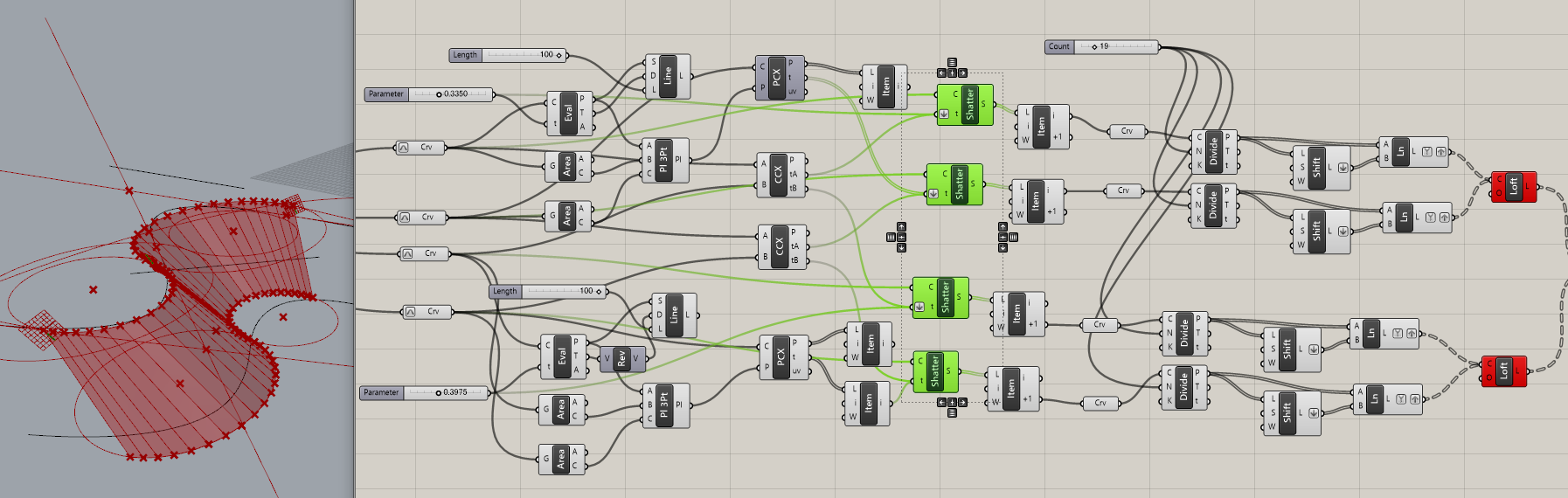
求めた分割点でShatterして、必要な側のカーブをListItemで取得します。
取得したカーブを等間隔に20個に分割し、ShiftListでリストをずらし、前後のポイントでラインを作成します。
最後にそれをロフトすると、面を貼ることができました。
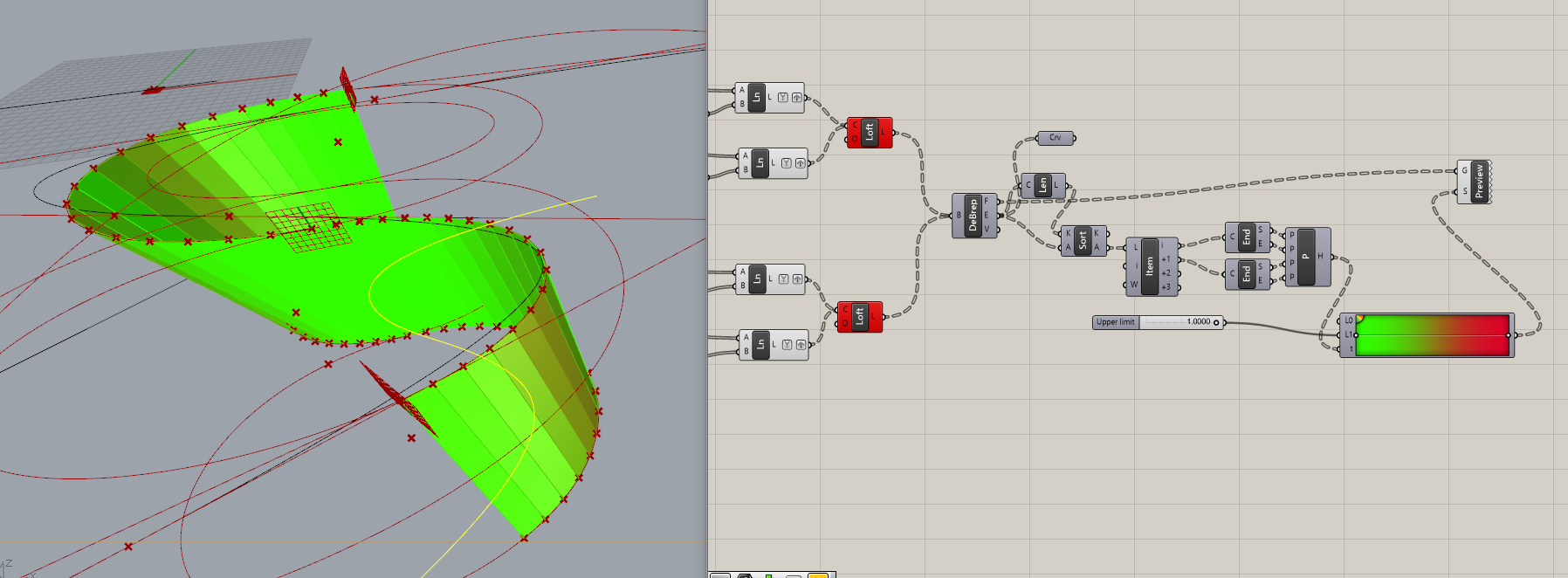
捻りをチェックすると、ほぼ捻りの無い面で構成されていることが分かると思います。
若干の捻りがありますが、これは厳密なコーンではないことから発生した捻りであるのではないかと思われます。
また、同じコーンのような形状でできているため、パネルのダブりが出ることでのコストダウンが見込めるのではないかと思います。
終わりに
ライノとGHを使うと、幾何学的形状を割と簡単に分析することができます。
形状の最適化や近似等様々なことができるので、重宝しています。
今後は有機的な形をいかに作るか等、時間のある限りアップロードしていけたらいいなと思っています。
施工者、設計者の役割についても私の数少ない経験上の話ですので、必ずしも正しいとは限りませんのでご容赦下さい。
また、今回のエクササイズの妥当性とか、本当に安いのかとかは検証していないので、あくまでサンプルとして捉えて頂けると幸いです。
それでは、また!