このブログについて
tomoarch.com は、建築・空間表現を軸に思考や実験を行っていた時期の記録です。
現在の制作・実装ベースの活動は Tomo Design Studio にて公開しています。
こんにちは!
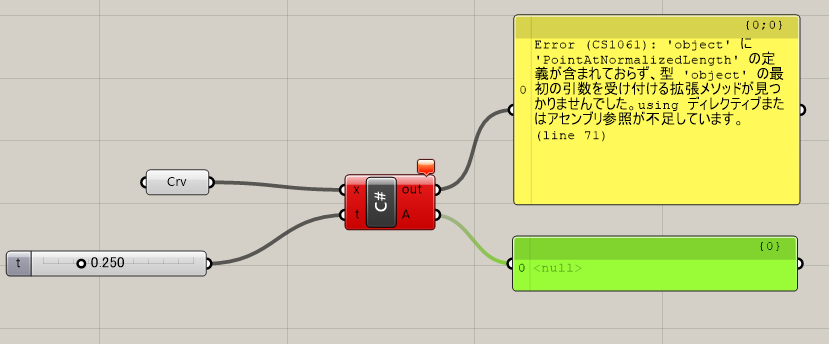
今日はgrasshopperでC#を使ったコンポーネントの作り方の応用について考えたいと思います。
参考にしたサイトはDesignalyze:Scripting in GHです。
このサイトは、たまに、アイフォンが当たりました!!とかいう詐欺サイトに飛ばされるので気を付けてください。
一つ目のコンポーネントはroundやformatを使ったメートルをインチに直すスクリプトです。
二つ目のコンポーネントは木を作るスクリプトになります。
三つ目はフラクタルの雪の結晶のような何かを作るスクリプトです。
応用といってもそんなに難しくないので、最後までお付き合いよろしくお願いいたします。
入門編はこちらです!
GrashopperのC#コンポーネントでRoundとformatを使う
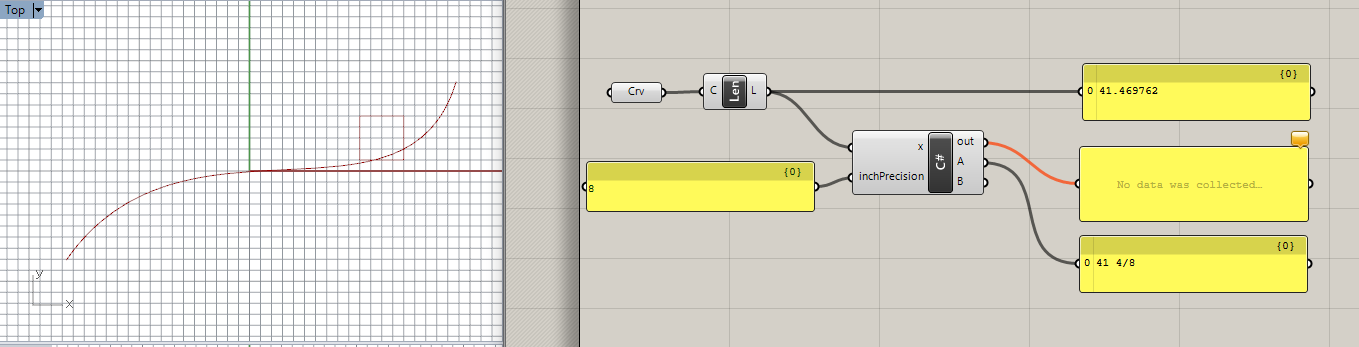
今回扱うコンポーネントは、メートル法をインペリアル(インチ)に直すコンポーネントです。
インチというのはご存じの通りアメリカで使われていて、5と1/4とか、7と31/32のように、2の倍数分の1で端数処理をします。
それをコンポーネントで実装したのがこのスクリプトになります。
下の図ではカーブの長さがメートル法では41.469762のところを、8で端数処理をした場合41と4/8になるということです。
inchPrecisionには2の倍数(2~32)を入れる事を想定しています。
さて、スクリプトの中を見てみましょう。
まず、wholeNumber はxが入力であるのに対し、xの整数部分になります。
よって、x-wholeNumberとは、端数部分になるということですね。
すると、(x-wholeNumber) * inchPrecision)は端数に例えば32をかけたものということになります。
そして、Math.Roundによってその端数を四捨五入します。
これで、きれいに32で割った時の分子ができるということになります。
int wholeNumber = (int) x;
double inchPart = Math.Round((x-wholeNumber) * inchPrecision);
if (inchPart == inchPrecision) {
inchPart = 0;
wholeNumber = wholeNumber + 1;
}
//チェック用の合計値メートル法
B = wholeNumber + (inchPart / inchPrecision);
string answer = String.Format("{0} {1}/{2}", wholeNumber, inchPart, inchPrecision);
A = answer;
ここでif文が一つ入ります。
これは何かというと、四捨五入した結果 32/32になったりすると、それはwholeNumber+1と変わりませんね。
よって、そういった例外処理を書いてあるということです。
Bにはチェック用のメートル法で四捨五入した結果が入っています。
String.Formatではどのように整数、分母、分子を表示するかを指定していますね。
Aはその結果を表示しています。
このスクリプトは以上になります。
けっこう簡単ですよね!
GrashopperのC#コンポーネントで木を作る
次のエクササイズは下のGIFのように木を作りたいと思います。
lengthが枝の長さ、branchAngleが枝の回転角(度)、branchScaleが枝の幹に対する長さ、numが枝分かれの回数です。
早速スクリプトを見ていきましょう。
今回のスクリプトは二つの部分に分かれています。
上が実行するスクリプト本体ですね。
下は、スクリプトで使用する関数が入っています。
//角度をラジアンに変換
double bAngRad = ((Math.PI / 180) * branchAngle);
List<Line> lines = new List<Line>();//リストの宣言
//木の幹を作成する
Point3d stPt = new Point3d(0, 0, 0);//原点の作成
Vector3d unitYvect = new Vector3d(0, 1, 0);//単位ベクトルの作成
Line ln0 = new Line(stPt, unitYvect, length);//ラインの作成
lines.Add(ln0);//リストに加える
//二つのリストを作成し、片方に先ほど作ったリストを入れる
List<Line> tempList = new List<Line>();
List<Line> tempList2 = new List<Line>();
tempList = lines;
int i = 0;
while(i < num){//下の処理をnumの回数だけ繰り返す
tempList2 = CreateBranch(tempList, branchScale, bAngRad);//枝ラインのリストを返す後述の関数の実行
tempList = tempList2;//tempListの再定義
lines.AddRange(tempList2);//AddRangeで複数の要素を同時にリストに追加する
i++;//iをインクリメント
}
A = lines;
勘の良い人ならコメントアウトしてある部分を読むだけで分かってしまうかもしれませんが、それぞれを解説していきます。
まず、上の本体スクリプトからです。
まずは角度をラジアンに変換して後の回転角に使えるようにしておきます。
そしてlinesというラインのリストを宣言(初期化)しておきます。
そこに木の幹(最初の一本)を作成しリストに追加します。
次に、ラインのリストを二つ作ります。
(何故二つ作るかというと、Whileの中の処理で、別関数で作成した枝を受けるリストと、次のwhileで使用するリストとを分けて分かり易くするためです。)
Whileではnumの数だけ以下の処理を繰り返します。
枝を作る関数CreateBranchを実行します。引数に(tempList, branchScale, bAngRad)を取っていますね。
そして、これをtempList2に代入します。
tempList2をtempListに代入し、次のwhileループに備えます。
それと同時にできた枝tempList2をLinesのリストに追加します。
//枝作成関数
public List<Line> CreateBranch(List<Line> lines, double bScale, double bAng)
{
List<Line> newLines = new List<Line>();
foreach(Line ln in lines){//リスト内の各ラインについて下記の処理を行う
//現在の幹にスケールをかけて枝の長さを取得する
double newLength = ln.Length * bScale;
//現在の幹のエンドポイントと接線方向の取得
Point3d endPt = ln.To;
Vector3d unitTan = ln.UnitTangent;
//二本の枝を作りそれぞれをbAng分だけエンドポイントに対して回転する。
Line ln1 = new Line(endPt, unitTan, newLength);//ライン1の作成
ln1.Transform(Rhino.Geometry.Transform.Rotation(bAng, endPt));//ライン1の回転
Line ln2 = new Line(endPt, unitTan, newLength);//ライン2の作成
ln2.Transform(Rhino.Geometry.Transform.Rotation(bAng * -1, endPt));//ライン2の回転(逆)
//リストにそれぞれのラインを追加する
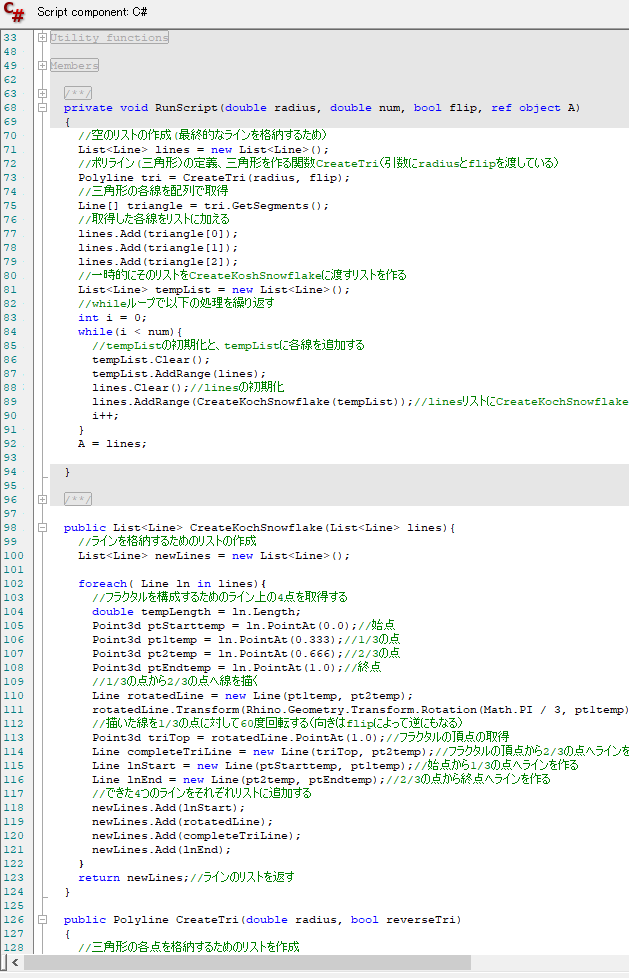
newLines.Add(ln1);
newLines.Add(ln2);
}
return newLines;//返り値に全てのラインのリストを返す
}
一方CreateBranch関数内では、templistで引数に代入された幹(枝)にスケールをかけて長さを取得し、そのエンドポイントと接線方向を取得して、エンドポイントを軸に回転(と逆回転)させた枝二本を取得します。
そして、その両方を返り値のリストに追加します。
これが作成された枝で、本体のtempList2に代入されるという仕組みになっています。
これで説明は大体できたかなと思います。
長い割には意外と明快にできていますよね!
次はフラクタルに挑戦です。
GrashopperのC#コンポーネントでフラクタルに挑戦する
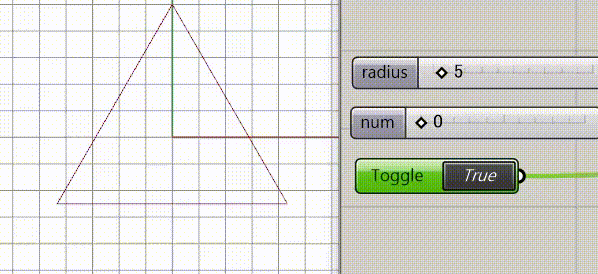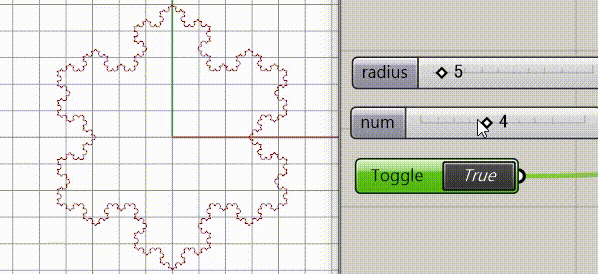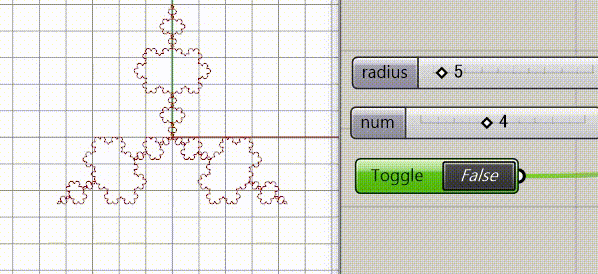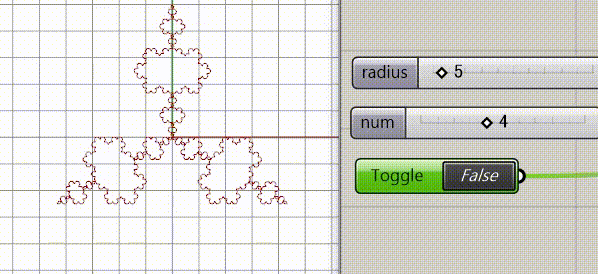
フラクタルは理解するのに少し時間を要しました。
スクリプト自体はとても簡単なのですが、図にするまでいまいちピンと来なかったので、図解したいと思います。
下は結果です。Radiusが半径numはフラクタルの回数です。トグルはフラクタルの向きを外側から内側にひっくり返すボタンです。
それでは早速スクリプトを見ていきましょう。
今回はメインのスクリプトに加えて、2つのスクリプトが存在します。
両方とも関数を定義していますが、1つ目は三角形を作るもので、もう1つはフラクタルのラインを生成するためのものです。
取り急ぎ全部貼ります。軽く目を通してから、細かく見ていきましょう。
メインのスクリプト
//空のリストの作成(最終的なラインを格納するため)
List<Line> lines = new List<Line>();
//ポリライン(三角形)の定義、三角形を作る関数CreateTri(引数にradiusとflipを渡している)
Polyline tri = CreateTri(radius, flip);
//三角形の各線を配列で取得
Line[] triangle = tri.GetSegments();
//取得した各線をリストに加える
lines.Add(triangle[0]);
lines.Add(triangle[1]);
lines.Add(triangle[2]);
//一時的にそのリストをCreateKoshSnowflakeに渡すリストを作る
List<Line> tempList = new List<Line>();
//whileループで以下の処理を繰り返す
int i = 0;
while(i < num){
//tempListの初期化と、tempListに各線を追加する
tempList.Clear();
tempList.AddRange(lines);
lines.Clear();//linesの初期化
lines.AddRange(CreateKochSnowflake(tempList));//linesリストにCreateKochSnowflakeで作成したラインを入れる(引数tempList)
i++;
}
A = lines;
フラクタルを作成する関数
public List<Line> CreateKochSnowflake(List<Line> lines){
//ラインを格納するためのリストの作成
List<Line> newLines = new List<Line>();
foreach( Line ln in lines){
//フラクタルを構成するためのライン上の4点を取得する
double tempLength = ln.Length;
Point3d ptStarttemp = ln.PointAt(0.0);//始点
Point3d pt1temp = ln.PointAt(0.333);//1/3の点
Point3d pt2temp = ln.PointAt(0.666);//2/3の点
Point3d ptEndtemp = ln.PointAt(1.0);//終点
//1/3の点から2/3の点へ線を描く
Line rotatedLine = new Line(pt1temp, pt2temp);
rotatedLine.Transform(Rhino.Geometry.Transform.Rotation(Math.PI / 3, pt1temp));
//描いた線を1/3の点に対して60度回転する(向きはflipによって逆にもなる)
Point3d triTop = rotatedLine.PointAt(1.0);//フラクタルの頂点の取得
Line completeTriLine = new Line(triTop, pt2temp);//フラクタルの頂点から2/3の点へラインを作る
Line lnStart = new Line(ptStarttemp, pt1temp);//始点から1/3の点へラインを作る
Line lnEnd = new Line(pt2temp, ptEndtemp);//2/3の点から終点へラインを作る
//できた4つのラインをそれぞれリストに追加する
newLines.Add(lnStart);
newLines.Add(rotatedLine);
newLines.Add(completeTriLine);
newLines.Add(lnEnd);
}
return newLines;//ラインのリストを返す
}
三角形を作る関数
public Polyline CreateTri(double radius, bool reverseTri)
{
//三角形の各点を格納するためのリストを作成
List<Point3d> pts = new List<Point3d>();
//三角形の各点を描くための原点から見た角度
const double ang0 = (Math.PI / 2);//90度
const double ang1 = (7 * Math.PI / 6);//210度
const double ang2 = (11 * Math.PI / 6);//330度
//三角形の各点の作成
Point3d pt0 = new Point3d(radius * Math.Cos(ang0), radius * Math.Sin(ang0), 0);
Point3d pt1 = new Point3d(radius * Math.Cos(ang1), radius * Math.Sin(ang1), 0);
Point3d pt2 = new Point3d(radius * Math.Cos(ang2), radius * Math.Sin(ang2), 0);
//各点をリストに入れる
pts.Add(pt0);
pts.Add(pt1);
pts.Add(pt2);
//ポリラインの宣言
Polyline pl = new Polyline();
//ポリラインの点リストにptsの各点を入れる
foreach(Point3d pt in pts){
pl.Add(pt);
}
//最後にポリラインを閉じるために一点目を追加する
pl.Add(pts[0]);
//三角形を描く方向を逆にする(フラクタルの頂点が内側に来るか外側に来るかがこれで決まる)
if(reverseTri == true){
pl.Reverse();//リスト内の点の順序を逆にする
}
return pl;//ポリライン(三角形)を返り値に返す
}
三角形を作る関数の解説
それでは、まずは一番最後の三角形を作る関数を解説します。
()の中はラジアンですね、度に直すと下記になります。
const double ang0 = (Math.PI / 2);//90度
const double ang1 = (7 * Math.PI / 6);//210度
const double ang2 = (11 * Math.PI / 6);//330度
この角度はいったい何の角度なの?と私は最初に思いましたが、下まで全部読むとここの角度だということが分かりました。
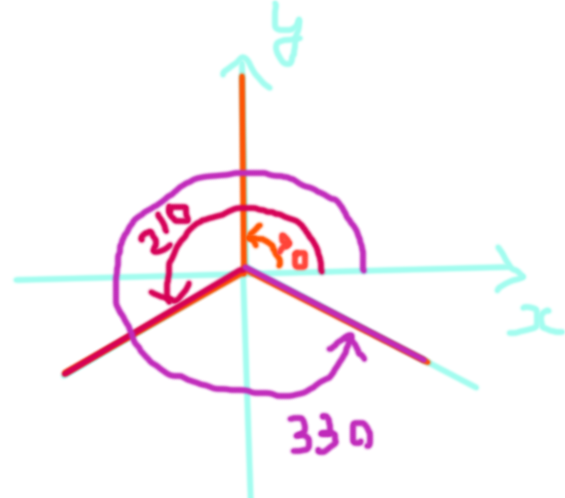
これで三角形の頂点を得るための角度を求めていますね。
Point3d pt0 = new Point3d(radius * Math.Cos(ang0), radius * Math.Sin(ang0), 0);
Point3d pt1 = new Point3d(radius * Math.Cos(ang1), radius * Math.Sin(ang1), 0);
Point3d pt2 = new Point3d(radius * Math.Cos(ang2), radius * Math.Sin(ang2), 0);
これはもちろん頂点のX,Y座標を求めて、点を作成していることになりますね。
そして、ポイント、0,1,2,0もしくはその逆0,2,1,0をbool値を利用して時計回りかそうでないか逆が取れるようにしてあります。
これによって、フラクタルの頂点が三角形の内側に来るか、外側に来るかを変更できるようにしてあります。
フラクタルを作る関数の解説
これも図解します、するとすごく簡単なことに気づきます。
フラクタルの関数では最初に直線の分割する点を作成していますね。
double tempLength = ln.Length; Point3d ptStarttemp = ln.PointAt(0.0);//始点
Point3d pt1temp = ln.PointAt(0.333);//1/3の点
Point3d pt2temp = ln.PointAt(0.666);//2/3の点
Point3d ptEndtemp = ln.PointAt(1.0);//終点
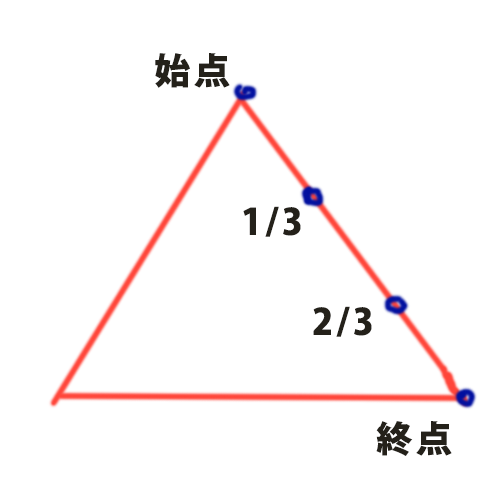
Line rotatedLine = new Line(pt1temp, pt2temp);
1/3の点から2/3の点へとラインを作ります。
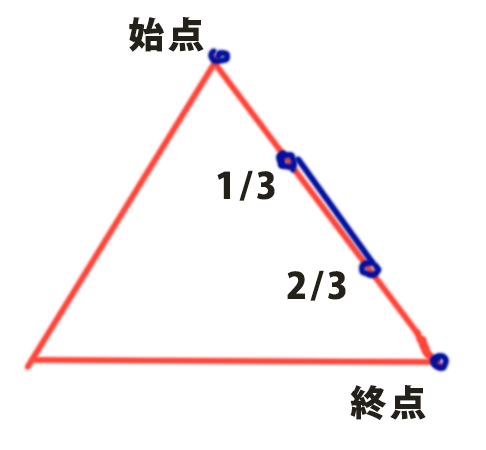
rotatedLine.Transform(Rhino.Geometry.Transform.Rotation(Math.PI / 3, pt1temp)); //描いた線を1/3の点に対して60度回転する(向きはflipによって逆にもなる)
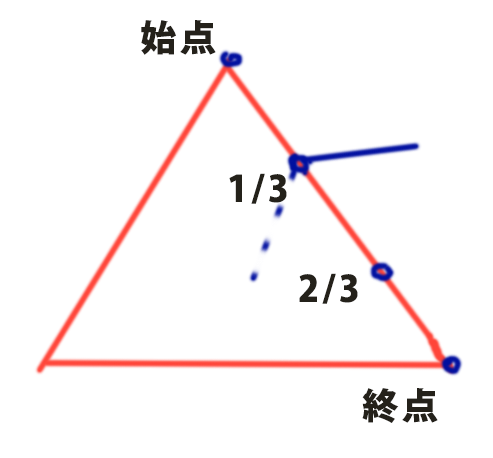
Point3d triTop = rotatedLine.PointAt(1.0);//フラクタルの頂点の取得
Line completeTriLine = new Line(triTop, pt2temp);//フラクタルの頂点から2/3の点へラインを作る
Line lnStart = new Line(ptStarttemp, pt1temp);//始点から1/3の点へラインを作る
Line lnEnd = new Line(pt2temp, ptEndtemp);//2/3の点から終点へラインを作る
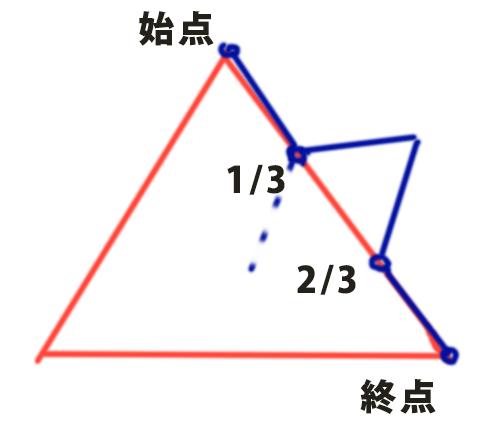
そして、できたこの4つの直線をリストに入れているだけです。
これをすべての線分について行うということですね。
メインのスクリプトの解説
メインのスクリプトではまずは3角形の関数を用いて、3角形を取得して、その線分を配列を用いて、リストに加えています。
そして、そのリストをCreateKoshSnowflakeに渡して、直線の分割とフラクタル化した線分のリストの取得をします。
そして、whileループでその処理を繰り返すといった流れになります。
どうでしょうか、うまくつながりましたでしょうか!
まとめ
今日は3つのエクササイズを通してGrasshopperのC#コンポーネントの応用について考察しました。
基本的な流れとしては、最初の部分にメインのスクリプトを入れて、後ろの方にサブの関数を仕込んであげるというのが定石のようですね。
いろいろと参考にできる部分が沢山あると思うので、今度は自分のオリジナルスクリプトを考えてみたいと思います。
ちょっと難しかった方は入門編もどうぞ。
それでは、また!!
※本記事は当時の思考・試行錯誤の記録です。
現在の制作・プロジェクトについては Tomo Design Studio をご覧ください。